Why can elements in the 3rd period exceed 8 valence electrons?
Sulfur can have 12 valence electrons in #SO_4^(2-)# and Chlorine has 10 in #[ClO_4]^-# Why?
Sulfur can have 12 valence electrons in
1 Answer
What's new in
Recall that the angular momentum quantum number
#" "color(white)(/)s, p, d, f, . . .#
#l = 0, 1, 2, 3, . . . , n-1# ,
i.e. that the maximum
#n = 1, 2, 3, . . . #
Hence, if we are on the third period, we introduce
This is especially notable in silicon, phosphorus, sulfur, and chlorine if we consider the third period.
Usage of those

This expansion of "orbital space" is known in, for example:
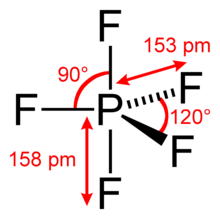
#"PF"_5# , where phosphorus has#10# valence electrons around it arranged in a trigonal bipyramidal geometry.
#"SF"_6# , where sulfur has#12# valence electrons around it arranged in an octahedral geometry.

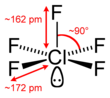
#"ClF"_5# , where chlorine has#12# valence electrons around it arranged in a square pyramidal geometry (two of which are in one lone pair).