Why do energy levels converge to a continuum and what is a continuum?
1 Answer
The continuum is simply a group of energy levels whose energy gaps are negligibly small, and it is reached when the kinetic energy of the electron(s) exceed the potential energy that would trap them.
Energy levels can only converge to a continuum when the potential energy that traps the electron is finite, or if it tapers off. When it is infinite, no continuum can occur.
DISCLAIMER: THIS IS A REFERENCE ANSWER!
The following are examples of potential energy wells commonly seen in quantum physics, with known energy solutions, that may or may not converge to a continuum:
1D FINITE SQUARE WELL
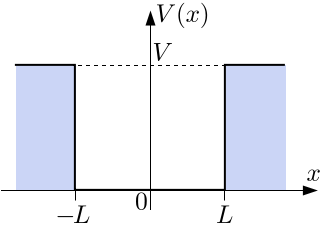
The potential energy is given by:
#V(x) = {(V_0, |x| >= L), (0, -L < x < L):}# where
#V_0# is a finite potential energy value. The box has length#2L# , and is centered at#x = 0# .
In this case,
This problem is generally solved in a piecewise manner, defining a wave function for the three sections of the potential energy well. The energy solutions are most easily determined by graphing to separately find the "odd" and "even" solutions.
The unified solution is:
#E_n = (ℏ^2v_n^2)/(2mL^2)# where
#v_n# is the quantum number for each energy level.
Because the well is finite,
The full solution is shown here, detailing exactly how you can solve this problem step-by-step from beginning to end, by setting up the wave functions for each section, making the proper substitutions, etc.
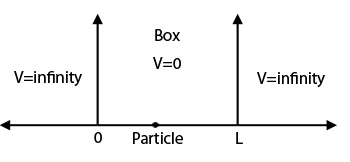
1D INFINITE WELL (PARTICLE IN A BOX)
The infinite well is an extension of the finite well for
Here, the potential energy is simply given by:
#V(x) = {(oo, |x| >= L), (0, -L < x < L):}#
This is probably the easiest kind of potential energy well problem you can solve, and you can do it on paper without a calculator.
The energy solution has a very familiar form:
#E_n = (ℏ^2n^2pi^2)/(2mL^2)#
The only difference is that
Here, we have no continuum because there is no end to how high this well actually is. We say that the particle can never penetrate into the "classical region", as
The full solution is shown here, solved from beginning to finish, including the Schrödinger equation for the problem.
It is a basic problem in quantum chemistry, and if you take that class, you must know how to do this inside and out.
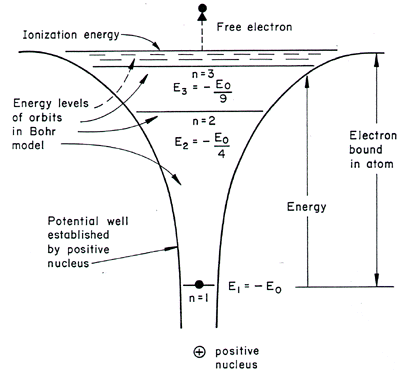
(3D) HYDROGEN ATOM
This is the most well-known problem, perhaps, and is well-applied in general chemistry; the potential energy well looks like this:
In this case, the potential energy is given by:
#V(r) = -(e^2)/(4piepsilon_0r)# where
#r = sqrt(x^2 + y^2 + z^2)# is a radial coordinate in a spherical coordinate system,#x = rsinthetacosphi# ,#y = rsinthetasinphi# , and#z = rcostheta# . The other symbols are known constants.
This problem is one of the most cumbersome ones to solve, and I go through about 90% of the solution here.
The energy solutions are given as:
#E_n = -(Z^2 m_e e^4)/(8h^2epsilon_0^2n^2)# or in easier units,
#E_n = -"13.6 eV" cdot Z^2/n^2# , where#Z# is the atomic number.
What we care about is that the energy goes as
What this means is that the atom is capably ionized, and