Will electrons pair up in an orbital only when all orbitals in different sub-levels have one electron?
1 Answer
Usually, yes, but not necessarily.
For a given
Hund's rule states that in order to maximize spin multiplicity, an atom usually fills one orbital at a time, and pairs up after every orbital of the same energy (or neighborhood of that energy) is half-filled.
Well, a counterexample is that thorium (
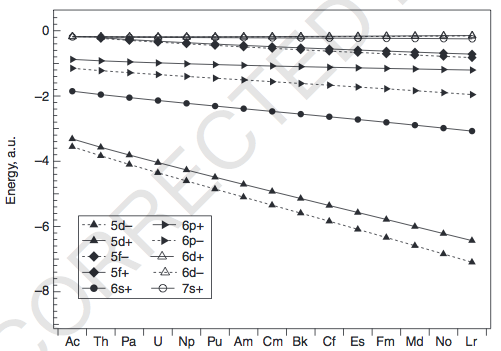
And yet, its electron configuration is:
#color(blue)([Rn]7s^2 6d^2 5f^0)#
rather than... (as lower
#[Rn]7s^2 6d^0 5f^2#
(Aufbau)
or... (as it decreases electron pairing interactions)
#[Rn]7s^1 6d^3 5f^0#
(Hund)
or even more seemingly reasonable... (as lower
#[Rn]7s^1 6d^0 5f^3#
(Aufbau + Hund)
And the reasoning behind that is the
The

