Question

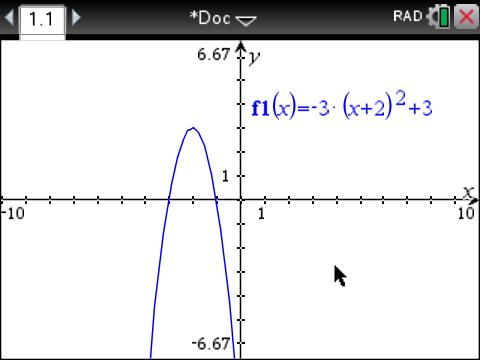
What is the vertex and direction of this parabola `y=-3(x+2)^2+3`?

Answer 1

`y=a(x-h)^2+k` has
vertex `(h,k)` and
opens up if `a` is positive (also written "if `a>0`")
opens down if `a` is negative ("if `a <0`")

`y=-3(x+2)^2+3` has `h = -2` , `k = 3` and `a = -3`

so the vertex is `(-2, 3)` and the parabola opens down.

Here's the graph:

graph{y = -3(x+2)^2+3 [-12.31, 10.2, -5.625, 5.625]}

Answer 2

A parabola in the form: `y = a(x - h)^2+k` will open up if a > 0, and down if a < 0. Since a = -3 in your example, the parabola will open down and have a maximum at the vertex.

In the form `y = a(x - h)^2+k`, (h,k) is the vertex. In your example, then, (-2,3) is the vertex. The maximum value is 3. Observe the graph below: