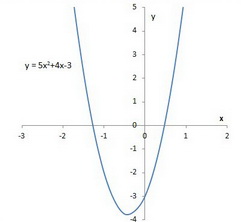
How do you find the vertex of #y = 5x^2 + 4x - 3#?

Question

3791 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-07-29T20:45:32

The vertex is at #color(red)((-2/5,-19/5)#.

#y = 5x^2+4x-3#

The standard form of the equation for a parabola is

#y = ax^2 + bx + c#

By comparing the two equations, we see that

#a = 5#, #b = 4#, and #c = -3#.

The #x#-coordinate of the vertex is at #x = -b/(2a) = -4/(2×5) = -4/10 = -2/5#.

To find the #y#-coordinate of the vertex, we insert #x = -2/5# into the equation.

#y = 5x^2+4x-3 = 5(-2/5)^2+4(-2/5)-3 = 5(4/25) -8/5-3#

#= 20/25-8/5-3 = 4/5-8/5-15/5= -19/5#

The vertex is at (#-2/5,-19/5#).

Graph