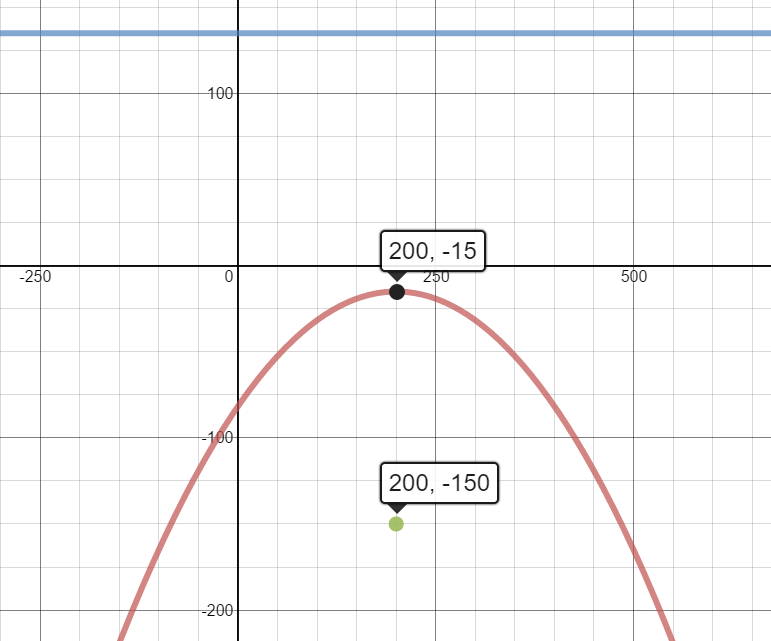
What is the vertex form of the equation of the parabola with a focus at (200,-150) and a directrix of #y=135 #?
1 Answer
Nov 22, 2015
The directrix is above the focus , so this is a parabola that opens downward .
Explanation:
The x-coordinate of the focus is also the x-coordinate of the vertex . So, we know that
Now, the y-coordinate of the vertex is halfway between the directrix and the focus:
vertex
The distance
Vertex form :
Inserting the values from above into the vertex form and remember that this is downward opening parabola so the sign is negative :
Hope that helped