Question

How would you find the area of an equilateral triangle using the Pythagorean Theorem?

Answer 1

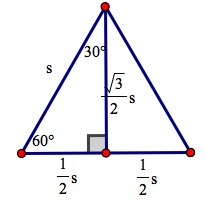
We can see that if we split an equilateral triangle in half, we are left with two congruent equilateral triangles. Thus, one of the legs of the triangle is `1/2s`, and the hypotenuse is `s`.

If we want to find the height, we use the Pythagorean Theorem:

`(1/2s)^2+h^2=(s)^2`
`1/4s^2+h^2=s^2`
`h^2=3/4s^2`
`h=sqrt3/2s`

If we want to determine the area of the entire triangle, we know that `A=1/2bh`. We also know that the base is `s` and the height is `sqrt3/2s`, so we can plug those in to the area equation to see the following for an equilateral triangle:

`A=1/2bh=>1/2(s)(sqrt3/2s)=(s^2sqrt3)/4`