An equilateral triangle is inscribed in a circle of radius 2. What is the area of the triangle?

Question

24369 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-12-14T20:46:35

#3sqrt3#

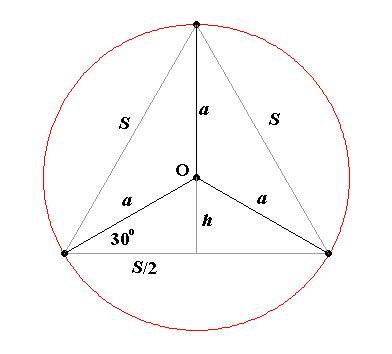
madisoncollege.edu

This is the scenario you've described, in which #a=2#.

Using the properties of #30˚-60˚-90˚# triangles, it can be determined that #h=1# and #s/2=sqrt3#.

Thus, #s=2sqrt3# and the height of the triangle can be found through #a+h=2+1=3#.

Note that the height can also be found through using #s# and #s/2# as a base and the hypotenuse of a right triangle where the other leg is #3#.

Thus, #A_"triangle"=1/2bh=1/2(2sqrt3)(3)=3sqrt3#.