A triangle has sides A, B, and C. If the angle between sides A and B is #(pi)/12#, the angle between sides B and C is #(2pi)/3#, and the length of B is 20, what is the area of the triangle?

Question

980 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-12-15T15:59:09

#100 sqrt 6 * sin frac{pi }{12}#

We use ABC for points; and a,b,c for opposite sides.

angle between a and b = #hat C = 1/12 pi#

angle between b and c = #hat A = 2/3 pi#

#hat B = pi - hat C - hat A = pi (1 - 1/12 - 2/3) = 1/4 pi#

Let #H in AC#, such that #BH# is perpendicular to #AC#.

#|BH| = h, |AH| = m# and we want #S_Delta = 1/2 * 20 * h#

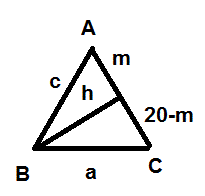
enter image source here

#tan hat A = h / m Rightarrow m = h / tan hat A#

#tan hat C = h / (20 - m) Rightarrow 20 - m = h / tan hat C#

#20 - h / tan hat A = h / tan hat C#

#20 = h ( 1 / tan hat A + 1 / tan hat C)#

#20 = h ( cos hat A / sin hat A + cos hat C / sin hat C)#

#h = 20 * frac{sin A sin C}{sin A cos C + sin C cos A} = 20/ sin frac{3 pi}{4} * sin frac{2 pi }{3} sin frac{pi}{12}#

#S_Delta = 10h = 200 * 2/sqrt 2 * sqrt 3 / 2 * sin frac{pi }{12}#