Iron crystallizes in a face-centered cubic system. If the radius of an iron atom is 1.26 A (angstroms), what is the edgelength of the unit cell? What is the density of iron if its atomic weight is 55.847 g/mole?
1 Answer
Here's what I got.
Explanation:
In order to be able to calculate the edge length of the unit cell, you need to start from the characteristics of a face-centered cubic system.
As you know, a face-centered cubic system is characterized by a unit cell that has a total of
- one lattice point for every one of the eight corners of the unit cell
- one lattice point for every one of the six faces of the unit cell
Now, these lattice points will contain
1/8"th"18th of an atom in every corner lattice point1/212 of an atom in every face lattice point
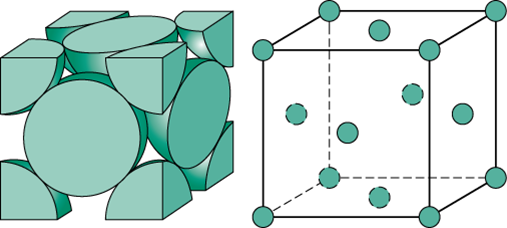 https://www.studyblue.com/notes/note/n/ceramics/deck/5172784
https://www.studyblue.com/notes/note/n/ceramics/deck/5172784
To calculate the edge length of the unit cell, you need to focus on one side of the cube. This face will look like this
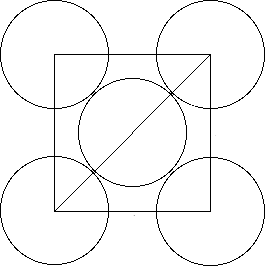 http://www.chemteam.info/Liquids&Solids/WS-fcc-AP.html
http://www.chemteam.info/Liquids&Solids/WS-fcc-AP.html
Let's say that
d^2 = x^2 + x^2d2=x2+x2
d^2 = 2x^2d2=2x2
The diagonal of the cell will be equal to one radius from the top-corner atom, two radii from the face atom, and one radius from the lower-corner atom
d = r + 2r + r = 4rd=r+2r+r=4r
This means that you have
(4r)^2 = 2x^2(4r)2=2x2
16 * r^2 = 2x^2 implies x = sqrt(8r^2)16⋅r2=2x2⇒x=√8r2
This is equivalent to
x = 2sqrt(2) * r = 2sqrt(2) * "1.26 A" = color(green)("3.56 A")x=2√2⋅r=2√2⋅1.26 A=3.56 A
So, the edge length of the unit cell is equal to
As you know, the density of a substance is defined as mass per unit of volume. This means that your goal now will be to find
- the mass of a unit cell
- the volume of a unit cell
Start by using Avogadro's number to determine the mass of a single atom of iron
55.847"g"/color(red)(cancel(color(black)("mol"))) * (1color(red)(cancel(color(black)("mol"))))/(6.022 * 10^(23)"atoms") = 9.274 * 10^(-23)"g/atom"
Next, use the aforementioned lattice points to determine how many atoms of iron you get per unit cell
"no. of atoms" = overbrace(1/8 xx 8)^(color(blue)("corner lattices")) + overbrace(1/2 xx 6)^(color(red)("face lattices")) = "4 atoms"
This means that the mass of a unit cell will be
9.274 * 10^(-23)"g"/color(red)(cancel(color(black)("atom"))) * (4color(red)(cancel(color(black)("atoms"))))/"unit cell" = 3.710 * 10^(-22)"g/unit cell"
Next, focus on finding the volume of a unit cell. As you know, the volume of a cube is given by the formula
color(blue)(V = l xx l xx l = l^3)" " , where
Now, convert the edge length of the unit cell from Angstroms to meters first, then from meters to centimeters by using the conversion factor
"1 A" = 10^(-1)"m"
3.56 color(red)(cancel(color(black)("A"))) * (10^(-10)color(red)(cancel(color(black)("m"))))/(1color(red)(cancel(color(black)("A")))) * "1 cm"/(10^(-2)color(red)(cancel(color(black)("m")))) = 3.56 * 10^(-8)"cm"
The volume of the unit cell will thus be
V = (3.56 * 10^(-8))^3"cm"^3
V = 4.512 * 10^(-23)"cm"^3
Finally, the density of iron will be equal to
color(blue)(rho = m/V)
rho = (3.710 * 10^(-22)"g")/(4.512 * 10^(-23)"cm"^3) = color(green)("8.22 g/cm"^3)
The answers are rounded to three sig figs, the number of sig figs you have for the radius of an iron atom.

