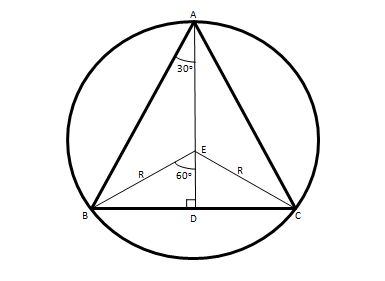
With reference to the figure above:
Considering the triangle ABD:
(Note: since the triangle ABC is equilateral, its internal angles are equal to #60^@#and a circle's radius with an endpoint in the triangle vertex A bisects the internal angle #B hat A C# in two angles, #B hat A D# and #D hat A C#, of #30^@# each.)
#tan B hat A D=tan 30^@=("side"/2)/(height)# => #height = "side"/(2*(sqrt(3)/3))=sqrt(3)/2*"side"#
#S_(triangle)=(("base")("height"))/2=(("side")(sqrt(3)/2)("side"))/2=(sqrt(3)/4)("side")^2# => #(cancel(sqrt(3))/4)("side")^2=4*cancel(sqrt(3))# => #("side")^2=16# => #side=4#
Considering the triangle BDE:
(Note that all the 3 triangles resulting from the division of the triangle ABC by the circle's radii with endpoints in A, B and C (triangles ABE, BCE and ACE) are congruent. So since their obtuse angles are equal and sum #360^@# (#A hat E B+B hat E C+A hat E C=360^@#), each one of them must be equal to #360^@/3=120^@#. Since the triangles BDE and CDE are congruents, #B hat E D=C hatE D#, and since they sum #120^@# (#=B hat E C#), each one of them is equal to #60^@#).
#sin B hat E D= sin 60^@=("side"/2)/R# => #R="side"/(2*sin 60^@)=(4)/(cancel(2)*sqrt(3)/cancel(2))=4/sqrt(3)#
Circle's Area
#S_(circ)=pi*R^2=pi*(4/sqrt(3))^2=(16/3)pi#


