Question

A triangle has sides A, B, and C. The angle between sides A and B is `(5pi)/6` and the angle between sides B and C is `pi/12`. If side B has a length of 1, what is the area of the triangle?

Answer 1

Sum of angles gives an isosceles triangle. Half of the enter side is calculated from `cos` and the height from `sin`. Area is found like that of a square (two triangles).

`Area=1/4`

Explanation:

The sum of all triangles in degrees is `180^o` in degrees or `π` in radians. Therefore:

`a+b+c=π`

`π/12+x+(5π)/6=π`

`x=π-π/12-(5π)/6`

`x=(12π)/12-π/12-(10π)/12`

`x=π/12`

We notice that the angles `a=b`. This means that the triangle is isosceles, which leads to `B=A=1`. The following image shows how the height opposite of `c` can be calculated:

For the `b` angle:

`sin15^o=h/A`

`h=A*sin15`

`h=sin15`

To calculate half of the `C`:

`cos15^o=(C/2)/A`

`(C/2)=A*cos15^o`

`(C/2)=cos15^o`

Therefore, the area can be calculated via the area of the square formed, as shown in the following image:

`Area=h*(C/2)`

`Area=sin15*cos15`

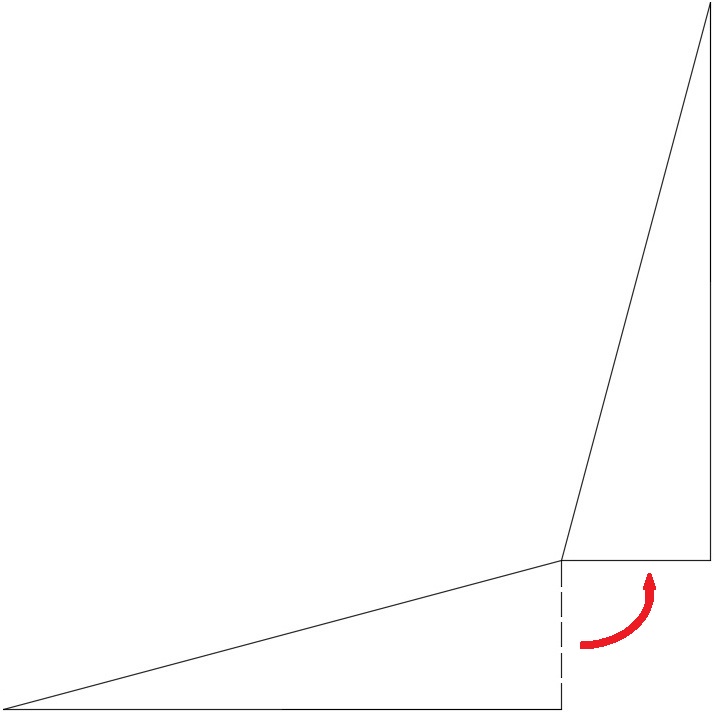
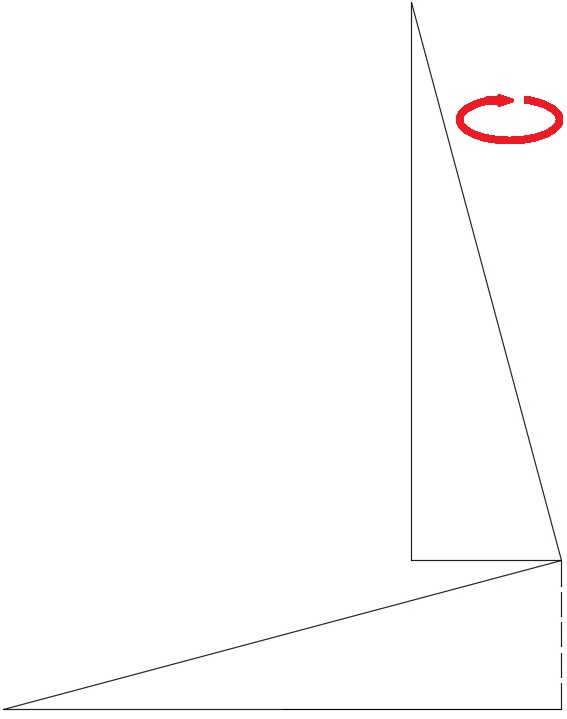
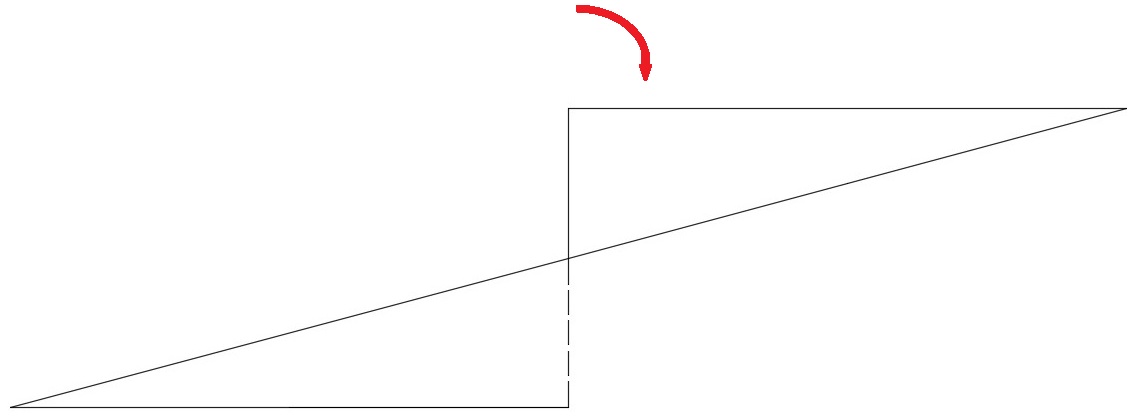
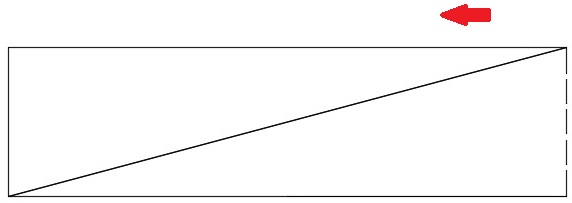
Since we know that:

`sin(2a)=2sinacosa`

`sinacosa=sin(2a)/2`

So, finally:

`Area=sin15*cos15`

`Area=sin(2*15)/2`

`Area=sin30/2`

`Area=(1/2)/2`

`Area=1/4`