A triangle has sides A,B, and C. If the angle between sides A and B is #(5pi)/8#, the angle between sides B and C is #pi/4#, and the length of B is 19, what is the area of the triangle?

Question

1906 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-01-14T12:29:10

Area #=1/2*19*32.44 ~~308.13#

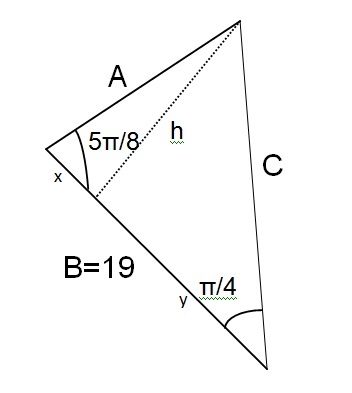
Sketch
The area of a triangle #=1/b*h# where #b = #base and #h=#height

In this case #tan((5pi)/8) =h/x# and #tan(pi/4) = h/y# where

#x+y = B =19#
#y=19-x#

So #xtan((5pi)/8) =ytan(pi/4)#
#xtan((5pi)/8) = (19-x)tan(pi/4)#
#x(tan((5pi)/8) +tan(pi/4)) = 19tan(pi/4)#

#:.x = 19tan(pi/4)/(tan((5pi)/8)+tan(pi/4))#

#h = (19tan(pi/4)/(tan((5pi)/8)+tan(pi/4)))tan((5pi)/8)#
#~~(19*1*2.414)/(2.414+1)#
#~~32.44#

Area #=1/2*19*32.44 ~~308.13#