Question

What are the components of the vector between the origin and the polar coordinate `(1, (5pi)/4)`?

Answer 1

The `x` component is: `cos((5pi)/4)`
The `y` component is: `sin((5pi)/4)`

Explanation:

Remembering our trigonometry, the vertical component of a vector is given by
`r*sin(theta)` where `r` is the length of the line,
and the horizontal component by
`r*cos(theta)`

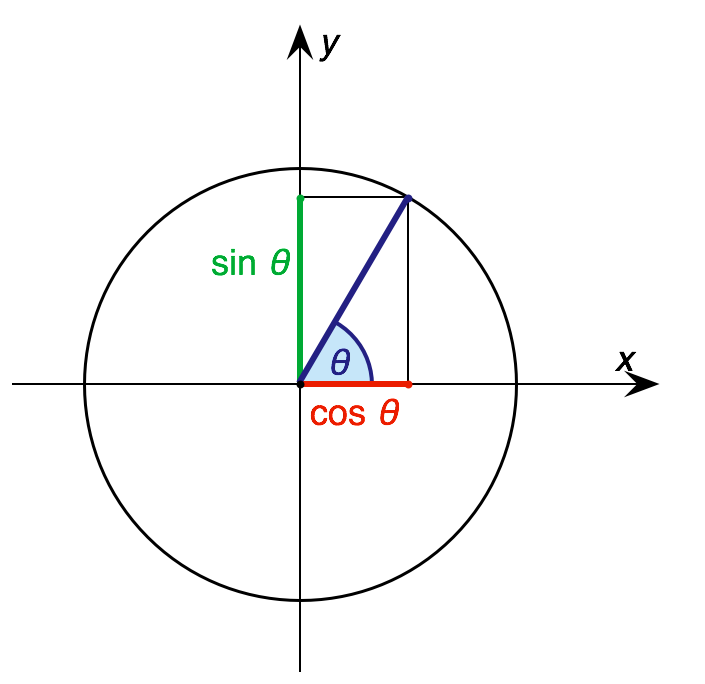
in the polar coordinate `(1,(5pi)/4)`, `r` is 1, and the angle `theta = (5pi)/4`.

Hence:
The `x` component is: `cos((5pi)/4)`
The `y` component is: `sin((5pi)/4)`

In this case, `(5pi)/4` is midway in the lower left quadrant, or `135^@`, so both are equal to `-1/sqrt2`