Question

A triangle has sides A, B, and C. The angle between sides A and B is `pi/3` and the angle between sides B and C is `pi/12`. If side B has a length of 1, what is the area of the triangle?

Answer 1

`A~~ 0.116`

Explanation:

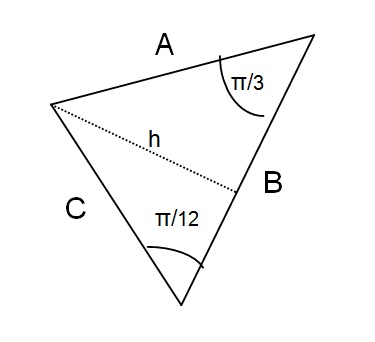Sketch
The area of a triangle `A = 1/2*Base*height`
In this case the base `B=1`
If we name the two portions of the base on either side of the perpendicular `h` as `x` and `y`, then `B = x+y = 1`

We then use the trigonometric relations
`h/x = tan(pi/12)`
`h/y =tan(pi/3)`

We now have three equations and three unknowns so we can solve to find `h`
`x = h/tan(pi/12)`
`y = h/tan(pi/3)`
`:.h/tan(pi/12) + h/tan(pi/3) = 1`

`h(tan(pi/3) + tan(pi/12))/(tan(pi/12)tan(pi/3)) = 1`

`:.h = (tan(pi/12)tan(pi/3))/(tan(pi/3) + tan(pi/12))`

`A = 1/2*1*(tan(pi/12)tan(pi/3))/(tan(pi/3) + tan(pi/12))`

`A~~( 0.268*1.732)/(2(1.732 + 0.268))`

`A~~ 0.464/4 ~~ 0.116`