Question

How do you expand `(1+x^3)^4` using Pascal’s Triangle?

Answer 1

Since there are (4 + 1) = 5 terms in this expansion, we must find the numbers located in the `5^(th)` term of the Pascal's Triangle. To find the number of terms in an expansion, always add 1 to the exponent, as to include the `0^(th)` term.

Explanation:

Draw a diagram to represent Pascal's Triangle. Each row is the sum of the numbers above it, with 1 at the first row, (1 and 1) at the second row, (1, 2 and 1) in the third row. The following diagram is of Pascal's Triangle:

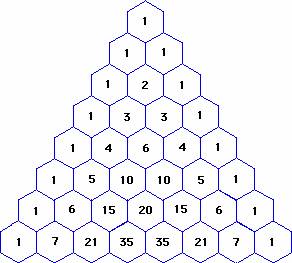
Counting up from the row with a single 1, we find that row 5 contains the numbers 1, 4, 6, 4 and 1.

To expand, the exponents on the 1 will start at 4 and will decrease until 0. The exponents on the `x^3` will increase from 0 to 4. As you can see, in each term the exponents must add up to the expression's exponent, which in this case is 4.

`1(1)^4(x^3)^0 + 4(1)^3(x^3)^1 + 6(1)^2(x^3)^2 + 4(1)^1(x^3)^3 + 1(1)^0(x^3)^4`

Simplifying by using exponent laws:

`1 + 4x^3 + 6x^6 + 4x^9 + x^12`

When fully expanded, `(1 + x^3)^4` = `1 + 4x^3 + 6x^6 + 4x^9 + x^12`. As you can see, in each t

Practice Exercises:

1. Expand `(2x - 3y)^5` using Pascal's Triangle.

2. Find the 3rd term in `(x + 3)^7`. Hint: Think of finding the appropriate number in the Pascal's Triangle and plugging it in for nCr in `t_(r + 1) = nCr(a)^(n - r) xx b^r`.

Good luck!