Cups A and B are cone shaped and have heights of 24 cm and 23 cm and openings with radii of 11 cm and 9 cm, respectively. If cup B is full and its contents are poured into cup A, will cup A overflow? If not how high will cup A be filled?
1 Answer
Mar 12, 2016
Explanation:
Volume of a cone is given by
Volume of cone A is
Volume of cone B is
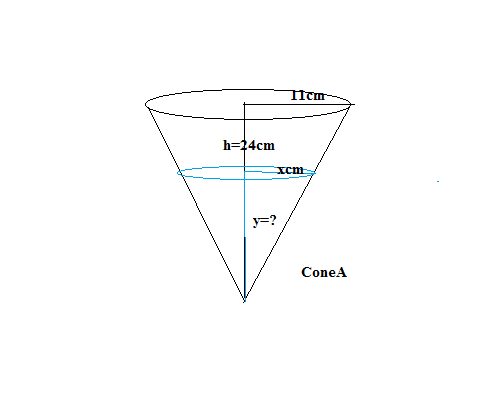
It is obvious that when contents of a full cone B are poured into cone A, it will not overflow. Let it reach where upper circular surface will form a circle of radius
then the relation becomes
So equating

