Question

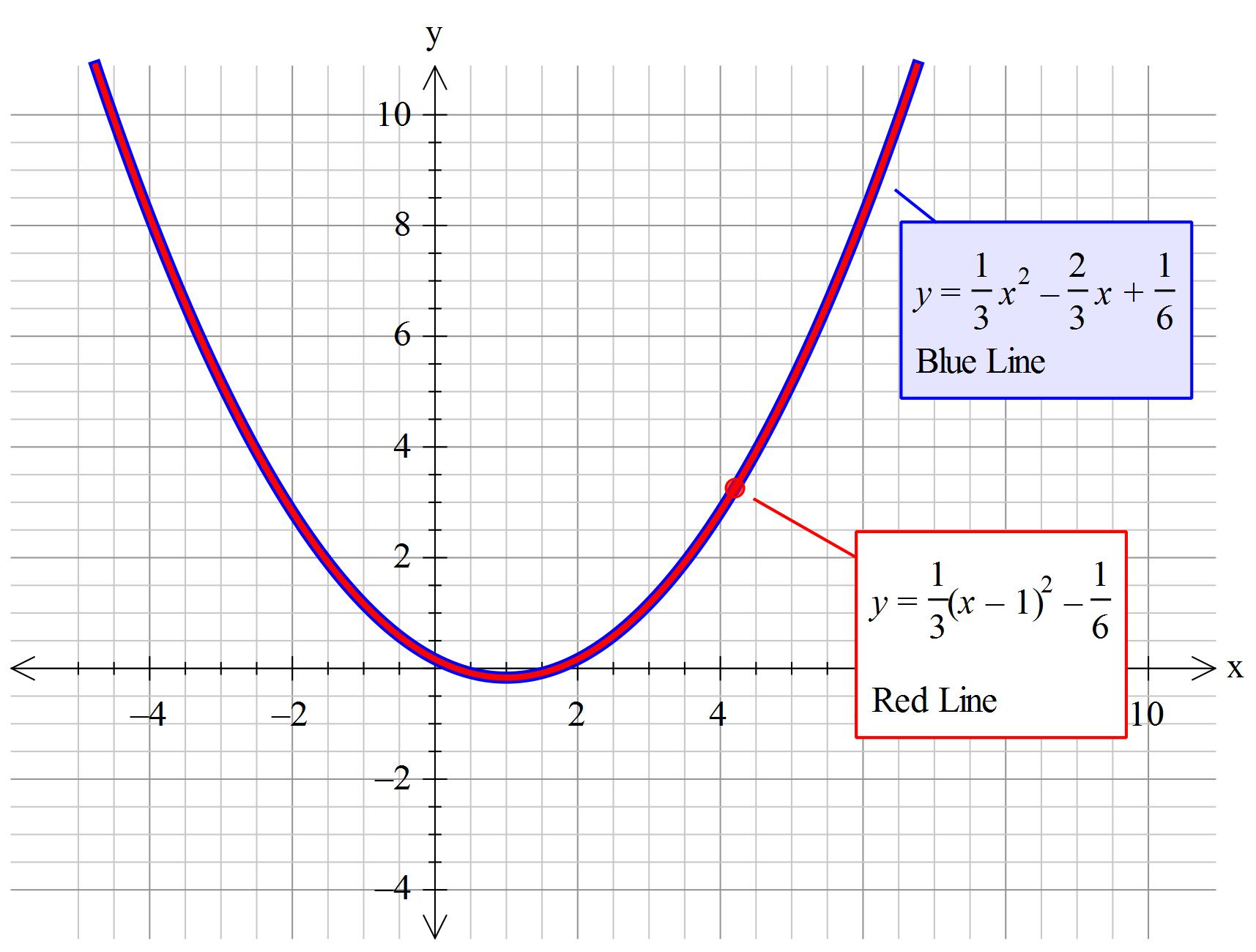
What is the vertex form of `y=1/3x^2 - 2/3x +1/6` ?

Answer 1

`color(red)(y=1/3(x-1)^2-1/6)`

Explanation:

Given:`" "y=1/3x^2-2/3x+1/6`..........................(1)

Write as:`" "y=1/3(x^2-2x)+1/6`

What we are about to do will introduce an error. Compensate for this error by adding a constant

Let `k` be a constant

`y=1/3(x^2-2x)+k+1/6`

`1/2` the coefficient of `x`

`y=1/3(x^2-x)+k+1/6`

'Get rid' of the single `x` leaving its coefficient of 1

`y=1/3(x^2-1)+k+1/6`

Move the index (power) of 2 to outside the brackets

`y=1/3(x-1)^2+k+1/6`...........................(2)

`color(brown)("This is your basic form. Now we need to find "k)`

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Consider the form `1/3(?-1)^2`. It produces the error of

`1/3xx(-1)^2 = +1/3`

To 'get rid' of this error we make `k=-1/3`

So equation (2) becomes

`y=1/3(x-1)^2 -1/3+1/6" "...........................(2_a)`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

`color(red)(y=1/3(x-1)^2-1/6)`