Question

How do you write a quadratic equation that passes through (0,9) and vertex is (-2,5)?

Answer 1

`y=(x+2)^2+5`
The other form of this is: `" "y=x^2+4x+9`

Explanation:

Standard form is:`" "y=ax^2+bx +c`

Vertex form is: `y=a(x+color(red)(d))^2+k`.................(1)

We know it passes through two points:

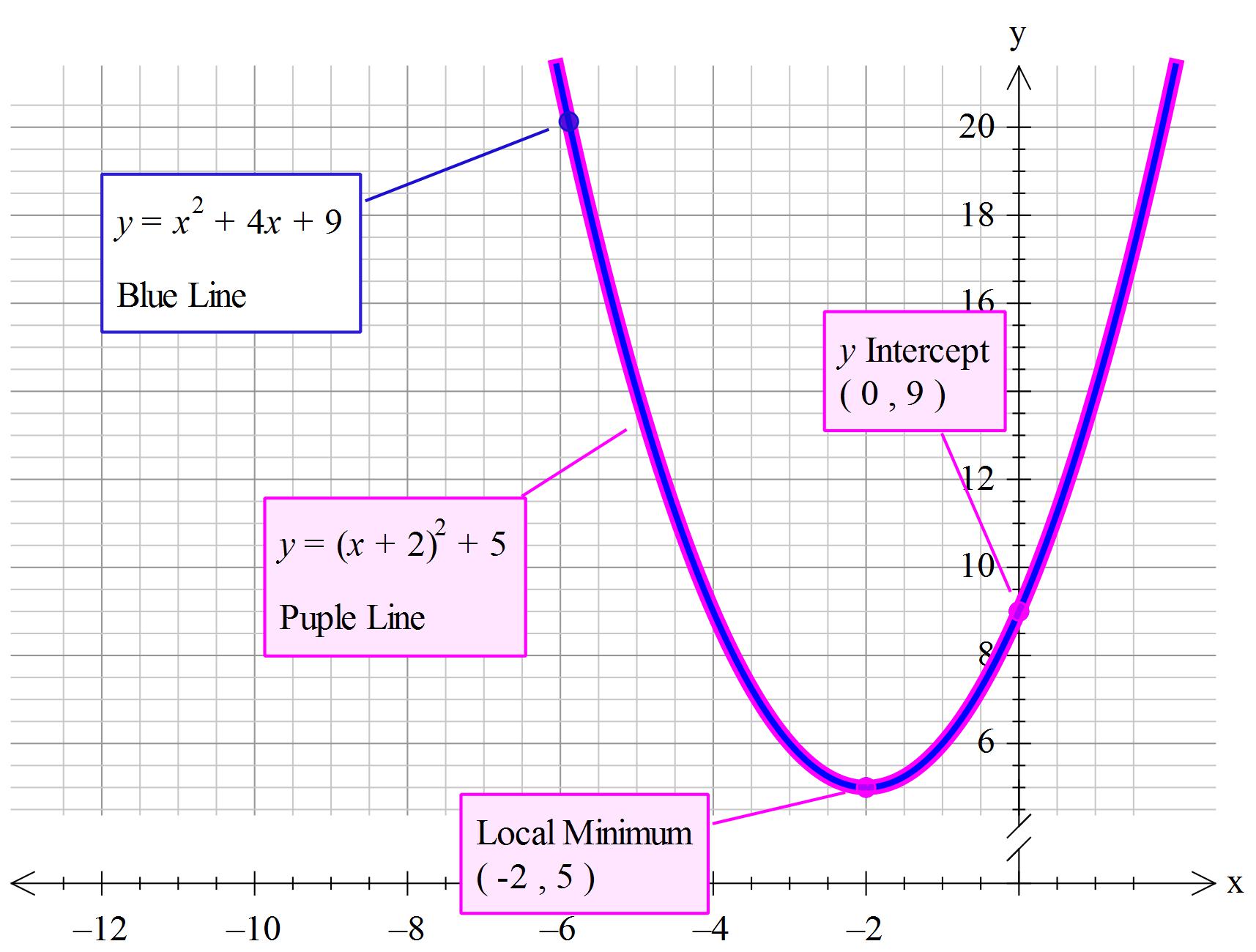
`P_1->(x_1,y_1)->(0,9)`

`color(brown)(P_2->(x_2,y_2)->(color(blue)(-2),color(magenta)(5)) -> Vertex)`

Known that `x_("vertex")=(-1)xxcolor(red)(d) =color(blue)(-2)` (in this case)

`=> d = +2`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Now we have:

`y=a(x+color(red)(2))^2+k`.................(2)

It is also known that `y_("vertex")=color(magenta)(5)` (in this case)

Thus equation (2) becomes

`y=a(x+color(red)(2))^2+color(magenta)(5)`.................(2)
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let us assume that `a =1` if it is not then the plot will not pass through `P_2`. As the plot does pass through this point then the completed equation is `y=(x+2)^2+5`

The equation can also be derived using the standard form of
`y=ax^2+bx+c`. Doing so would involve a lot more work.