Why do aromatic rings absorb light?
1 Answer
Everything we see absorbs light (otherwise, everything we see would be white). Thus, it's not surprising that aromatic rings do as well, since we can see them. But the question is not asked in the right way.
HOMO-LUMO GAPS
Aromatic rings, especially the larger, highly-conjugated
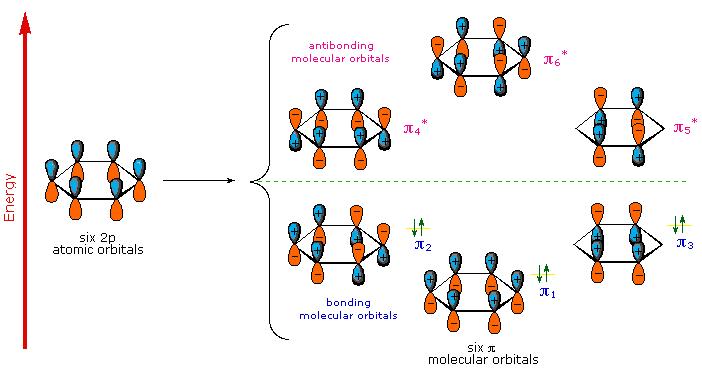
For instance, the
WE SEE EMITTED, NOT ABSORBED LIGHT
Recall that absorbed light is NOT what we see; we see emitted light, due to the relaxation of the excited electrons.
That is, if only blue light is absorbed, we see orange, the complementary color. If all light is absorbed, we see black.
It just so happens that some (but not all) fluorescent aromatic rings have HOMO-LUMO energy gaps that lie in the visible range of frequencies, thus emitting visible light upon relaxation of the excited electrons.
In this diagram, the four-benzene-ring molecule (tetracene) absorbs light in the visible range (
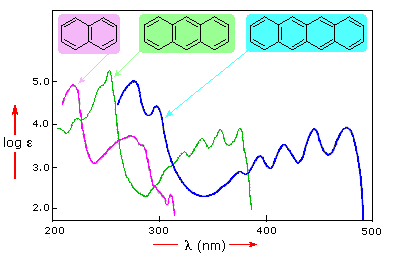
But you see based on the two-benzene-ring and three-benzene-ring molecules that not all aromatic compounds emit visible light...
COLORLESS EXAMPLE
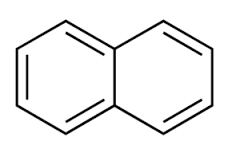
For instance, diacene's (a.k.a. napthalene) calculated HOMO-LUMO gap is
#"4.74 eV" xx (1.6027xx10^(-19) "J")/("1 eV") = 7.593xx10^(-19) "J"#
Now, converting that to
Recall the equation to convert energy to wavelength:
#\mathbf(E) = hnu = \mathbf((hc)/lambda)# where:
#E# is the energy in#"J"# .#h = 6.626xx10^(-34) "J"cdot"s"# is Planck's constant.#c = 2.998xx10^(8) "m/s"# is the speed of light.#lambda# is the wavelength in#"m"# .
Thus, we get:
#color(green)(lambda) = (hc)/E#
#= ((2.998xx10^(8) "m/s")(6.626xx10^(-34) "J"cdot"s"))/(7.593xx10^(-19) "J")#
#= 2.6160xx10^(-7) "m"#
#~~# #color(green)("262 nm")#
It's in the hundreds of
COLORED EXAMPLE
Something that IS colored is tetracene, which is four benzene rings connected adjacently by their bonds (rather than by single carbons).
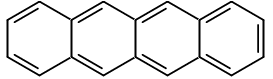
The HOMO-LUMO gap for tetracene from DFT-calculations (pg. 17) is said to be
So, the corresponding wavelength is:
#color(green)(lambda) = (hc)/E#
#= ((2.998xx10^(8) "m/s")(6.626xx10^(-34) "J"cdot"s"))/("2.74 eV" xx (1.6027xx10^(-19) "J")/("1 eV"))#
#= 4.524xx10^(-7) "m"#
#~~# #color(green)("452 nm")#
This is absorbing blu-ish light, so it looks orange (see bottom of page).
And if we extend to pentacene (5 adjacent benzene rings), we would get
Notice the pattern from the paper:
#E_"gap, diacene"^"KS" ~~ "4.74 eV" harr "262 nm"#
#E_"gap, triacene"^"KS" ~~ "3.54 eV" harr "350 nm"#
#E_"gap, tetracene"^"KS" ~~ "2.74 eV" harr "452 nm"#
#E_"gap, pentacene"^"KS" ~~ "2.19 eV" harr "566 nm"#
#E_"gap, hexacene"^"KS" ~~ "1.78 eV" harr "696 nm"#
And ALL of these are in the
The HOMO-LUMO gap converges for larger and larger conjugated

