Question #6e951
1 Answer
Here's what I got.
Explanation:
!! LONG ANSWER !!
The idea here is that you can decrease the concentration of a solution by increasing its volume while keeping the number of moles of solute constant.
This is the underlying principle of a dilution. In order to dilute a solution, you must make sure that you keep the number of moles of solute constant and proceed to increase the total volume of the solution.
Since doing this would leave you with the same number of moles of solute in a bigger volume, the target solution will be less concentrated than the starting solution, i.e. more dilute.
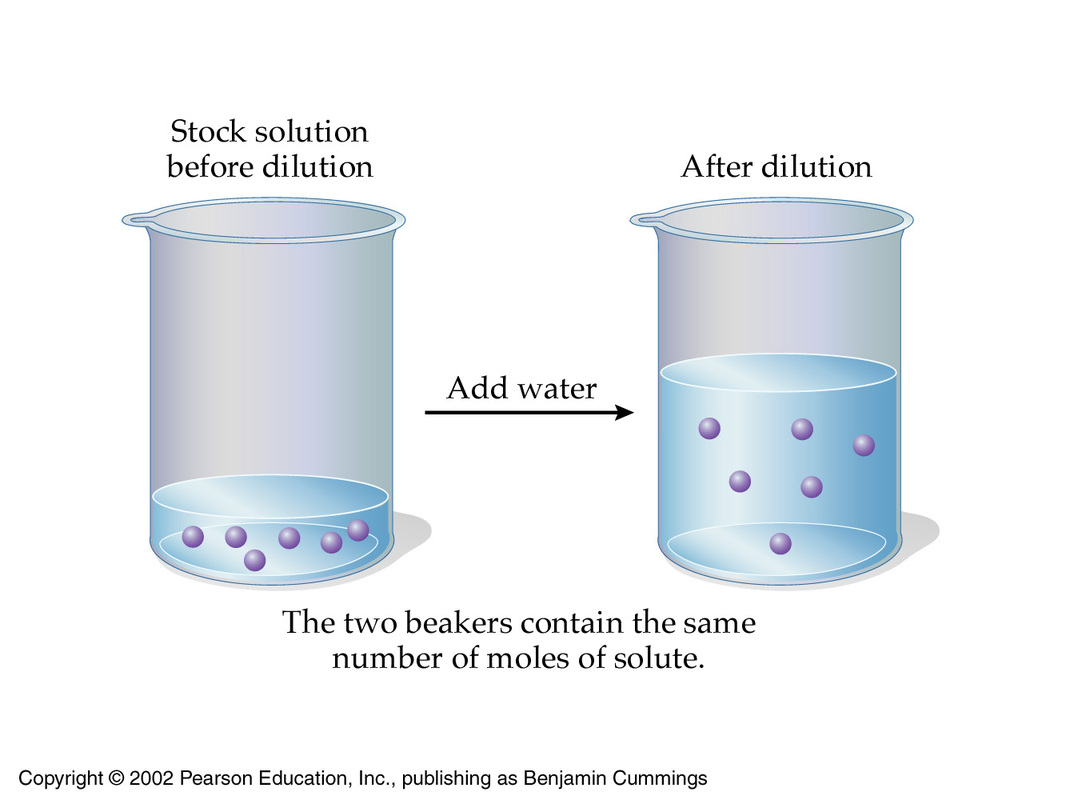
Now, you're dealing with two solutions labeled
As you know, a solution's molarity tells you how many moles of solute you get per liter of solution.
Use the molarities and volumes of the two solutions to determine how many moles of solute you get
#color(purple)(|bar(ul(color(white)(a/a)color(black)(c = n_"solute"/V_"solution" implies n_"solute" = c * V_"solution")color(white)(a/a)|)))#
You will have
#"For A: " n_A = "1.00 mol" color(red)(cancel(color(black)("L"^(-1)))) * overbrace(100 * 10^(-3)color(red)(cancel(color(black)("L"))))^(color(blue)("volume in liters")) = "0.10 moles A"#
#"For B: " n_B = "2.00 mol" color(red)(cancel(color(black)("L"^(-1)))) * overbrace(200 * 10^(-3)color(red)(cancel(color(black)("L"))))^(color(blue)("volume in liters")) = "0.40 moles B"#
Now, you mix these two solutions and add an extra
#V_"total" = V_A + V_B + V_"water"#
#V_"total" = "100 mL" + "200 mL" + "100 mL" = "400 mL"#
Now all you have to do is use the known numbers of moles of solute to determine the new concentrations of
#"For A: " c_A = "0.10 moles"/(400 * 10^(-3)"L") = color(green)(|bar(ul(color(white)(a/a)"0.25 mol L"^(-1)color(white)(a/a)|)))#
#"For B: " c_B = "0.40 moles"/(400 * 10^(-3)"L") = color(green)(|bar(ul(color(white)(a/a)"1.0 mol L"^(-1)color(white)(a/a)|)))#
I'll leave the answers rounded to two sig figs.
ALTERNATIVE APPROACH
Alternatively, you can get the same result a bit quicker by using the dilution factor, which essentially tells you how much concentrated the initial solution was compared with the dilute solution.
If you keep in mind the idea that the number of moles of solute remains constant in a dilution, you can use the formula for molarity to write
You can express this by using molarities and volumes
#color(blue)(overbrace(c_1 xx V_1)^(color(orange)("moles of solute in concentrated solution")) = overbrace(c_2 xx V_2)^(color(orange)("moles of solute in diluted solution"))#
Here
Rearrange this equation to get
#c_1V_1 = c_2V_2 implies c_1/c_2 = V_2/V_1#
This represents your dilution factor
#color(blue)(|bar(ul(color(white)(a/a)"D.F." = c_1/c_2 = V_2/V_1color(white)(a/a)|)))#
Let's take solution
#"For A: " "D.F." = (400 color(red)(cancel(color(black)("mL"))))/(100color(red)(cancel(color(black)("mL")))) = 4#
Therefore, the initial solution was
#"D.F." = c_1/c_2 implies c_2 = c_1/"D.F." = "1.00 mol L"^(-1)/4 = color(green)(|bar(ul(color(white)(a/a)"0.25 mol L"^(-1)color(white)(a/a)|)))#
Now look at solution
#"D.F." = (400color(red)(cancel(color(black)("mL"))))/(200color(red)(cancel(color(black)("mL")))) = 2#
Its final concentration will thus be
#c_2 = c_1/"D.F." = "2.00 mol L"^(-1)/2 = color(green)(|bar(ul(color(white)(a/a)"1.0 mol L"^(-1)color(white)(a/a)|)))#

