Question

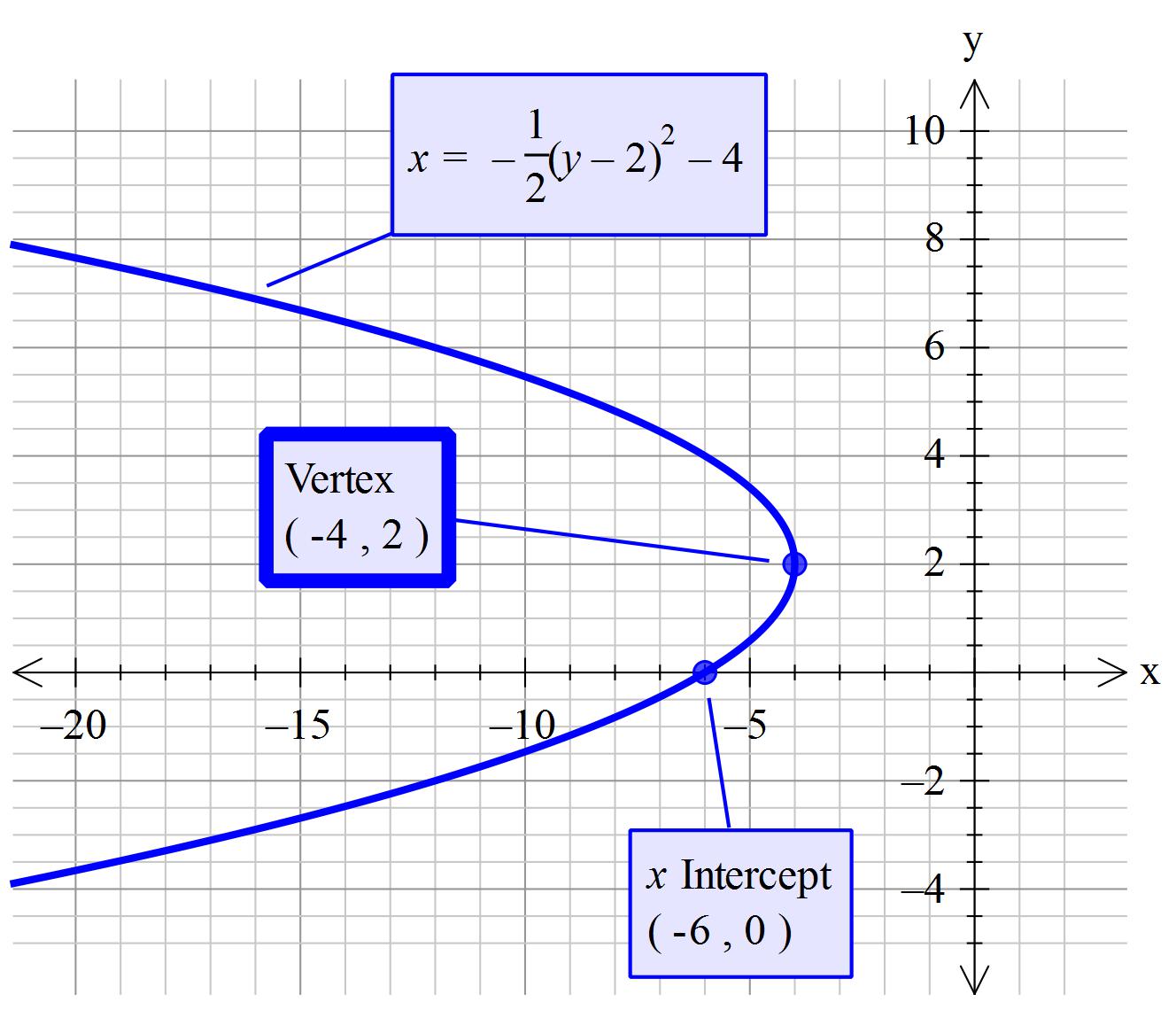
How do you find the vertex and intercepts for `x =-1/2(y-2)^2-4`?

Answer 1

`color(blue)("Vertex "->(x,y)->(-4,2))`
`color(blue)(x_("intercept")=-6)`
`color(blue)(y_("intercept")=2+-(2sqrt(2)) i color(red)(" "y_("intercept")!inRR`

(No 'Real Number' solution for y intercept)

Explanation:

Instead of an equation in `x` we have an equation in `y`. What that does is 'rotate' the graph `90^o` to the right

So instead the general shape being `nn` it is `sup`

Also the format of the given equation is in Vertex form.

`color(blue)("Determine the vertex")`
'..................................................................
`color(red)("If this had been an equation in "x) color(magenta)(larr" For comparison only")`

Then `color(red)(x_("vertex")=(-1)xx(-2) = +2)`

`color(red)(y_("vertex")=-4`
'.......................................................................

But our equation is in `y` so we need to reverse them in that

`color(green)(y_("vertex")=(-1)xx(-2)=+2)`
`color(green)(x_("vertex")=-4)`

`color(blue)("Vertex "->(x,y)->(-4,2))`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

`color(blue)("Determine x intercept")`

Set `y=0` giving

`color(brown)(x=-1/2(y-2)^2-4)color(green)(" "->" "x=-1/2(0-2)^2-4`

`color(blue)(x_("intercept")=-6)`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Determine y intercept")`

Set `x=0`

`color(brown)(x=-1/2(y-2)^2-4)color(green)(" "->" "0=-1/2(y-2)^2-4`

Add 4 to both sides

`4=-1/2(y-2)^2`

Multiply both sides by (-2)

`-8=(y-2)^2`

Square root both sides

`sqrt(-8)=y-2`

`y=2+-sqrt(-8)`

As you have square root of a negative number the graph does not cross the y axis.

So the only solution for the values of y are in the complex numbers set of values

`y=2+-(2sqrt(2)) i`