Question

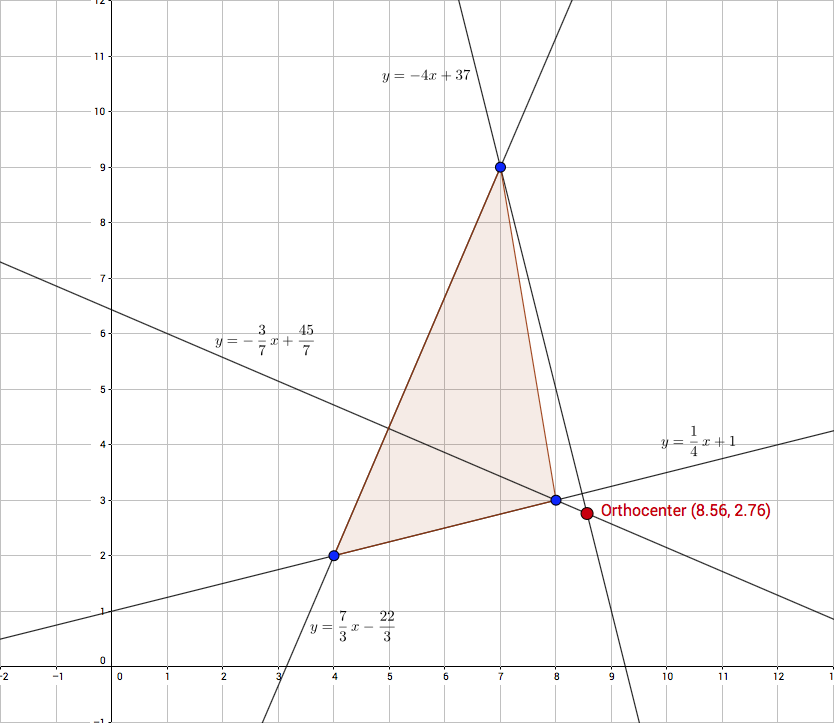
What is the orthocenter of a triangle with corners at `(4 ,2 )`, `(8 ,3 )`, and (7 ,9 )#?

Answer 1

It is `(8.56, 2.76)`.

Explanation:

The orthocenter is the intersection of the lines perpendicular to the sides passing from the opposite vertex.

The first step is to calculate the line passing from two of the corners.
The general equation of a line is `y=mx+q`. This line has to pass by two points at the same time, so we substitute the points and observe what we have:

`2=4m+q`
`3=8m+q`

we can subtract the first equation from the second, side by side

`3-2=8m-4m+q-q` that becomes
`1=4m` and then `m=1/4`

I plug this value on the first equation to find `q`

`2=4*1/4+q` obtaining `q=1`
The line passing from the first two points is: `y=1/4x+1`.
Now we want the orthogonal to this line.
As any other line on the plane, the equation of the orthogonal is `y=mx+q`, and we immediately know the `m` because two perpendicular lines has the angular coefficients inverse and reciprocal. Then the `m` of the line was `1/4` and the `m` of the orthogonal is `-4`.
We have to find only `q`. For this purpose we need to fix a point and the point that we want is the third one in the triangle. I plug `(7,9)` in the equation of the orthogonal

`9=-4*7+q`
`q=37`

So the orthogonal passing from the third point is

`y=-4x+37`.

We repeat the same procedure taking the point 1 and 3 and finding the line.

`2=4m+q`
`9=7m+q`
subtract the first from the second
`7=3m` and `m=7/3`
`2=4*7/3+q` and `q=-22/3`
The equation of the line between point 1 and 3 is then
`y=7/3x-22/3`.

The orthogonal has an `m=-3/7` and has to pass by point 2

`3=-3/7*8+q` and `q=45/7`
The orthogonal line is then `y=-3/7x+45/7`.

Now we need to intersect both the orthogonal and we will have the orthocenter. Technically the orthocenter is the intersection of the three perpendicular, but we do not need to calculate the third because a point is fully identified already with the intersection of two lines.
We intersect

`y=-4x+37`
`y=-3/7x+45/7`

having
`-4x+37=-3/7x+45/7`
`3/7x-4x=45/7-37`
`25/7x=214/7`
`x=214/25`

substituting the valute of `x` in one of the two equations I have

`y=-4*214/25+37`
`y=69/25`.

The orthocenter has coordinates `(214/25, 69/25)` or in decimal form `(8.56, 2.76)`.