Question

Two opposite sides of a parallelogram have lengths of `5`. If one corner of the parallelogram has an angle of `pi/4` and the parallelogram's area is `45`, how long are the other two sides?

Answer 1

Here is a diagram.

Explanation:

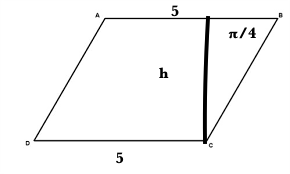
The area of a parallelogram is given by `a = b xx h`.

We know the base and the area, as shows the diagram above. However, we need to find the height.

`45 = 5 xx h`

`9 = h`

Now, we can use right angled trig to find the length of the other side. We know the side opposite `pi/4` (9), and we want to find the hypotenuse. Therefore, we will be using sin, because `sintheta = "opposite"/"hypotenuse"`

`(sin(pi/4))/1 = 9/(BC)`

By special angles, `sin(pi/4) = 1/sqrt(2)`

Therefore, `BC = 9/(1/sqrt(2))`

`BC = 9sqrt(2)`

So, the other two sides measure `9sqrt(2)` units.

Hopefully this helps!