Question

A parallelogram has sides with lengths of `14` and `9`. If the parallelogram's area is `42`, what is the length of its longest diagonal?

Answer 1

Here is a diagram.

Explanation:

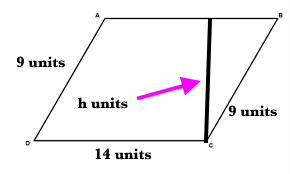
The image shows that the height of this parallelogram is unknown. The formula for area of a parallelogram is `a = b xx h`. We know the base, and we know the area, so we can solve for height.

`a = b xx h`

`42 = 14 xx h`

`42/14 = h`

`3 = h`

`:.` The height of the parallelogram is 3 units.

Now that we know two sides, we can use SOHCAHTOA to determine the measure of angle B.

We know the side opposite B and the hypotenuse. We will therefore use `sin`.

`sinB = 3/9`

`B = 19˚`

Since opposite angles in parallelograms have equal measures, we can conclude that `B = D = 19˚, "or" B + D = 38˚`.

The total angles in a parallelogram add up to `360˚`, so we can state that

`A + C = 360 - 38, A = C`

Solving the system of equations:

`A + A = 322`

`2A = 322`

`A = 161˚`

Now that we know the measure of A, the length of `AB` and the length of `AD`, we can use cosine's law to determine the length of `BD`.

`BD^2 = AD^2 + AB^2 - 2ADAB(cosA)`

`BD^2 = 9^2 + 14^2 - 2(9)(14)(cos(161˚))`

`BD ~~ 22.70`

`:.` The length of the longest diagonal is approximately `22.70` units.

Hopefully this helps!