Question

How do you solve the system by graphing `y= 1/4x -1` and `y= -2x -10`?

Answer 1

`x=-4`
`y=-2`

Explanation:

the given system

`y=1/4x-1`

`y=-2x-10`

Solution

`y=y`

`1/4x-1=-2x-10`

Transpose all terms with x on the left side

`1/4x+2x=-10+1`

`(1/4+2)x=-9`

`9/4x=-9`

Multiply now both sides by 4/9

`4/9*9/4x=4/9(-9)`

`x=-4`

to solve for `y` use equation `y=-2x-10` and `x=-4`

`y=-2x-10`

`y=-2(-4)-10`

`y=8-10`

`y=-2`

Checking

With equation `y=1/4x-1`

`y=1/4x-1`

`-2=1/4(-4)-1`

`-2=-2" "`correct

~~~~~~~~~~~~~~~~~~~~~~~

Checking

With equation `y=-2x-10`

`y=-2x-10`

`-2=-2(-4)-10`

`-2=-2" "`correct

God bless....I hope the explanation is useful

Answer 2

Solution by graphing below.
`color(white)("XXX")(x,y)~~(-4,-2)`

Explanation:

For each of the given equations select a few (at least two but I would suggest three) values for `x` and solve for corresponding `y` values.

#{: (color(red)(y=1/4x-1),,," | ",color(blue)(y=-2x-10),,), (,color(red)(underline(x)),color(white)("X")color(red)(underline(y))," | ",,color(white)("X")color(blue)(underline(x)),color(white)("X")color(blue)(underline(y))), (,color(red)(0),color(red)(-1)," | ",,color(white)("X")color(blue)(0),color(blue)(-10)), (,color(red)(4),color(white)("X")color(red)(0)," | ",,color(white)("X")color(blue)(1),color(blue)(-12)), (,color(red)(8),color(white)("X")color(red)(1)," | ",,color(blue)(-1),color(white)("X")color(blue)(-8)) :}#

Plot each pair of points which you have calculated and draw a line for each equation's set of points.

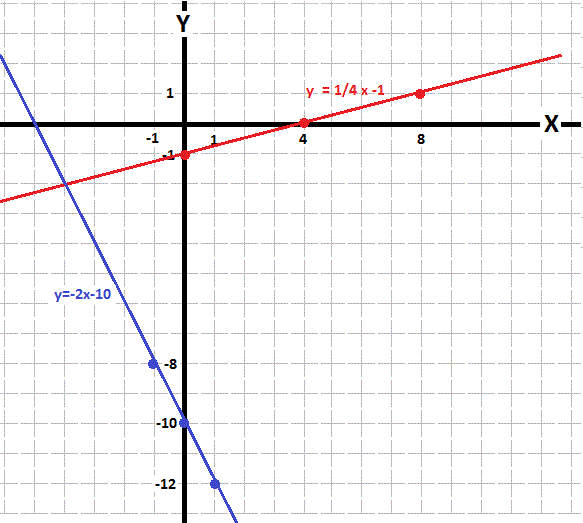
The point where the two equation lines intersect provide the coordinates of the system solution.

In this case it appears that `x` is about `-4` and `y` is about `-2`.
(This in fact the exact solution but, in general, solving equations by graphing is very dependent on the accuracy of your drawing).