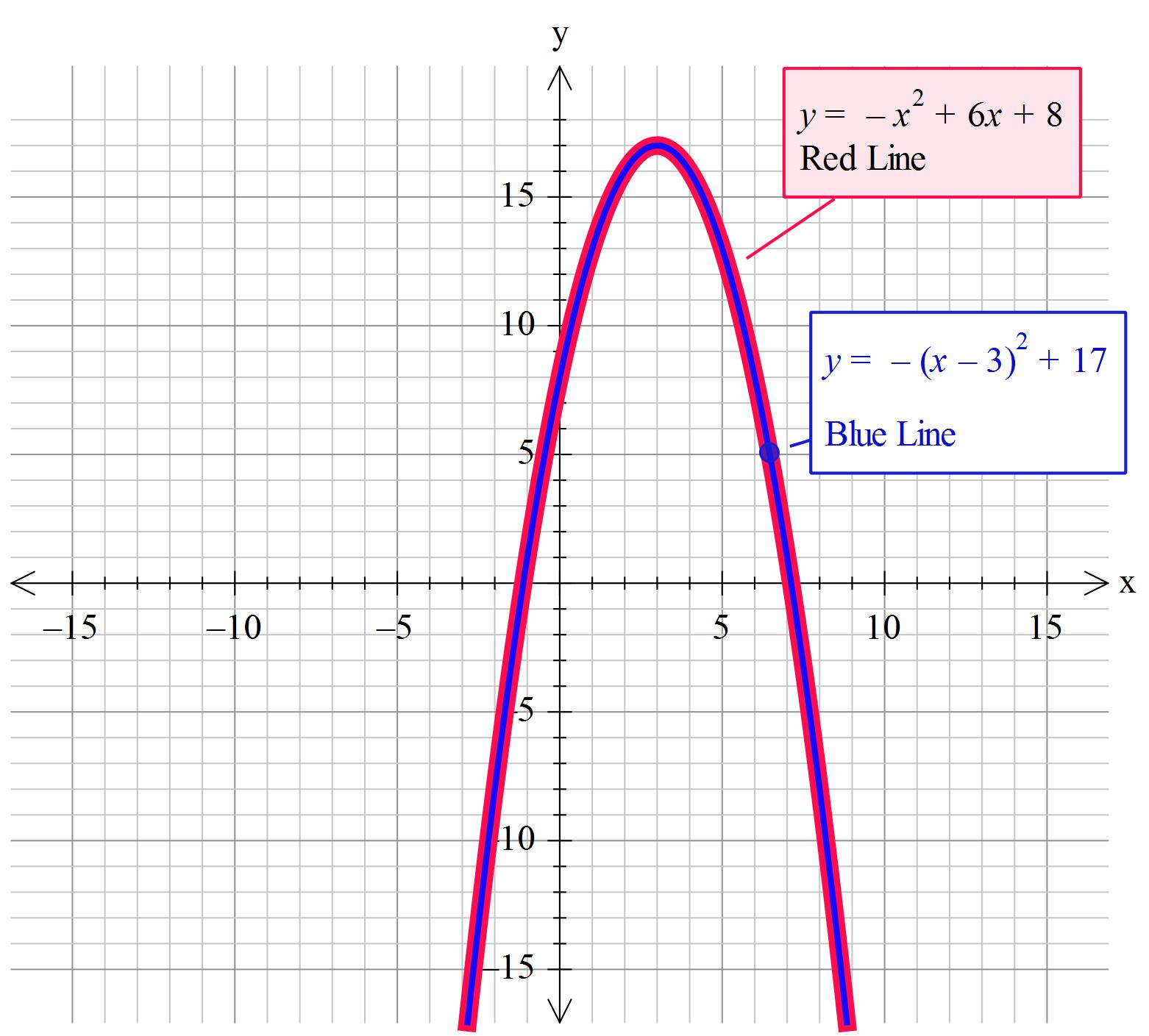
This process introduces an error that has to be compensated for by the inclusion of the correction factor of #k#. This has to be so to maintain the truth of the expression being equal that of y.
In that #f(x)=-x^2+6x+8+k# at this stage #k=0#
Write as:#y=( -1x^2+6x)+8+k#
Factor out the #-1# (Sometimes this value is not 1)
#y=-1(x^2-6x)+8+k#
take the exponent (power of 2) outside the bracket
#y=-1(x-6x)^2+8+k" "larr" now "k" comes into effect."#
Note that each step the value of #k# changes until we finish modifying at which point it becomes a constant.
Halve the coefficient of #-6x#
#y=-1(x-3x)^2+8+k#
Discard the #x# from #-3x#
#y=-1(x-3)^2+8+k" "larr" nearly there. "k" is now fixed"#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
If you were to expand the bracket and compere to the original equation you would observe that there is an extra value. This is from squaring the #-3# from inside the bracket. #k# cancels that out.
Let #(-3)^2+k=0" "=>" "k=-9#
#color(brown)("However we have a -1 outside the bracket so this becomes.")#
Let #(-1)(-3)^2+k=0" "=>" "k=+9#
#color(brown)(y=-1(x-3)^2+8+k)color(blue)(->y=-1(x-3)^2+17#
Write as:#" "y=-(x-3)^2+17#