Question

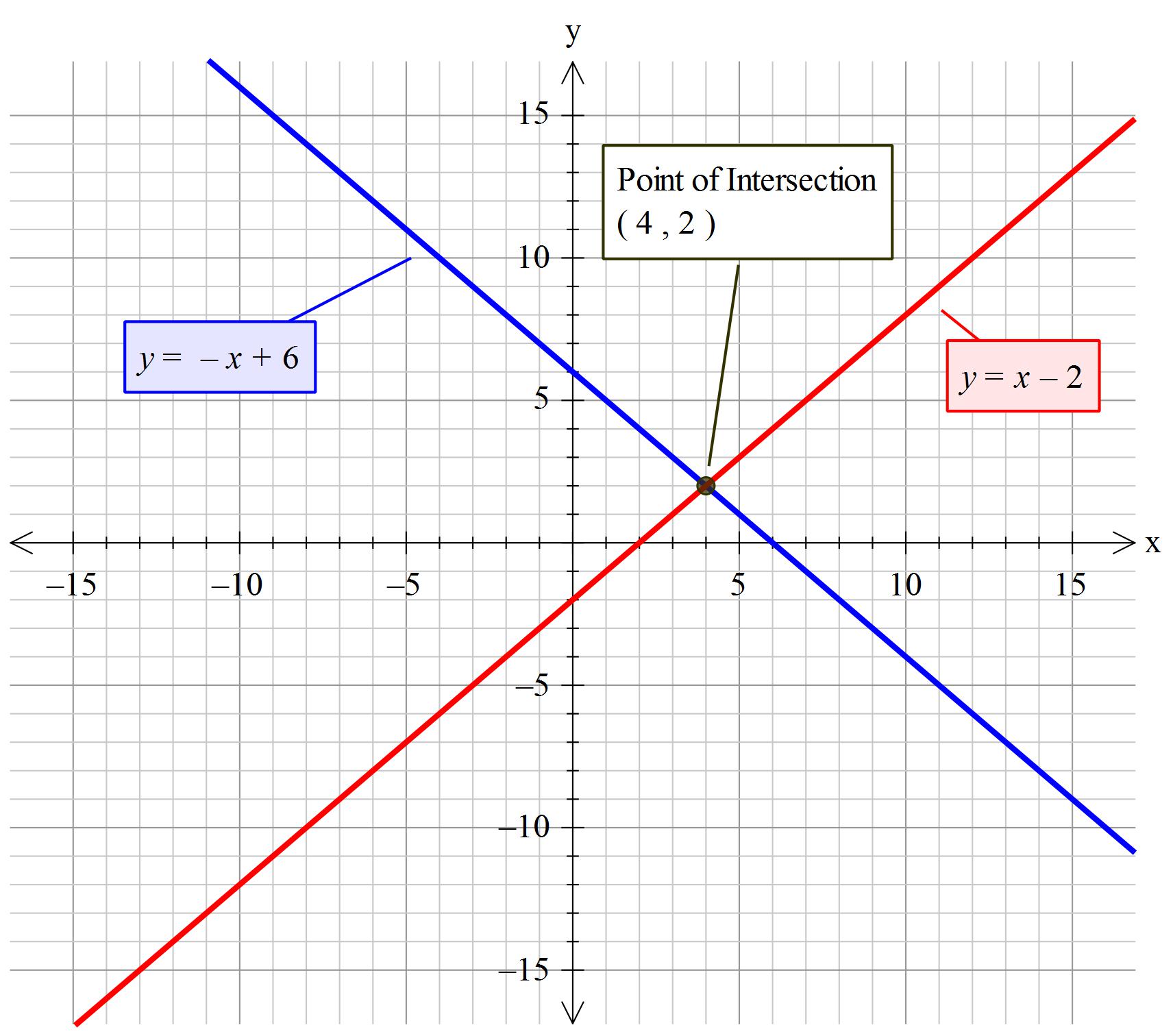
How do you solve the system `x+y=6` and `x-y=2` by graphing?

Answer 1

The common point ( point of intersection) is: `(x,y)->(4,2)`

Explanation:

Simultaneous equations are such that (normally) they plot a range of value that are different to each other. That is, until they cross . At that instant the both have the same values for `x" and "y`. They must have to be able to 'occupy' the same point. For some equation types it can be more than one point and for others, no point at all.

`color(blue)("To determine value of "x)`

Write as:

`x+y=6`
`ul(x-y=2)" "larr" add to and up with only 1 unknown"`
`2x+0=8`

Divide both sides by 2

Thus `x=4`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

`color(blue)("To determine value of "y)`

Substitute `x=4` into `x+y=6" "`giving:

`color(brown)(x+y=6) " "color(blue)(->" "4+y=6)`

Subtract 4 from both sides

`color(brown)(4color(blue)(-4)+y=6color(blue)(-4))`

`0+y=2`

`y=2`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~