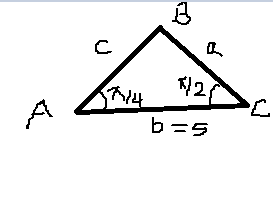
A triangle has sides A, B, and C. The angle between sides A and B is #(pi)/2# and the angle between sides B and C is #pi/4#. If side B has a length of 5, what is the area of the triangle?

1 Answer
bp
Jul 10, 2016

25/2

Explanation:

The figure below is how the triangle has been described. For the area of the triangle, length of the perpendicular on base 'b' needs to be determined. For doing this use sine formula to find side 'a'

#sinA/a= sinB/b# Angle B is #pi-pi/2-pi/4= pi/4#

therefore # (sinpi/4)/a= (sinpi/4)/5#

This gives a=5. Therefore length of the perp. from vertex B on side b would be 5 #sin (pi/2)# = 5

Area of Triangle = #1/2 (5) (5) =25/2#

enter image source here

Related questions
See all questions in Area of a Triangle
Impact of this question
1340 views around the world
You can reuse this answer
Creative Commons License