Question

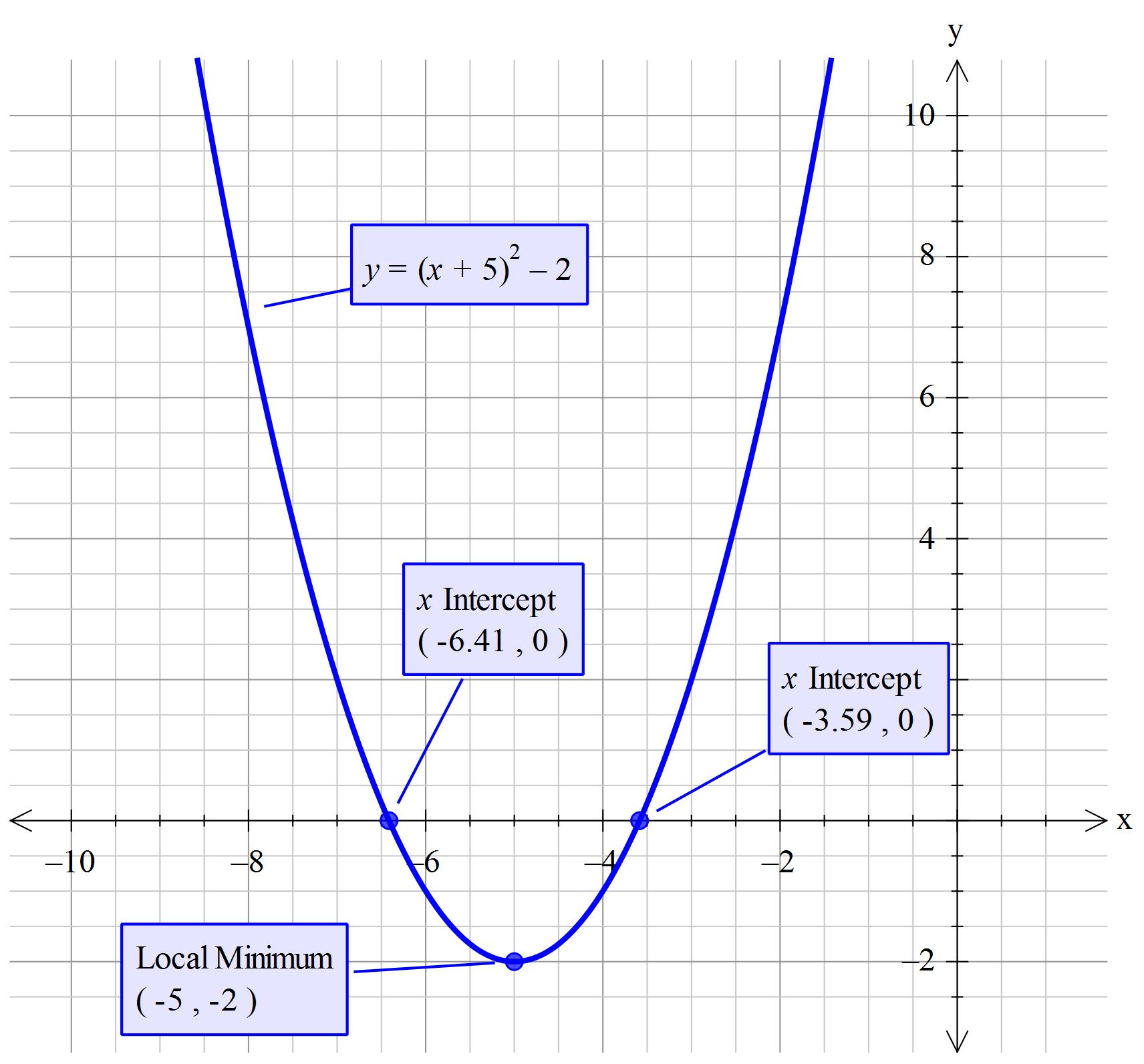
How do you find the vertex and intercepts for `y = (x + 5)^2 – 2`?

Answer 1

Vertex->(x,y)=(-5,-2)#

`y_("intercept")->y=23`

`x_("intercept")` as follows:
`x=-5+-sqrt(2)`

`x~~-6.414` to 3 decimal places
`x~~-3.586` to 3 decimal places

Explanation:

`color(blue)("Determine the vertex")`

This is already in a vertex form the of quadratic equation so you can read off the coordinates of the vertex directly.

`x_("vertex")=(-1)xx(+5) = -5`
`y_("vertex")=-2`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Determine y intercept")`

y intercept is at `x=0`

`=>y=(0+5)^2-2 -> y=23`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Determine x intercept")`

Set `y=0` giving

`0=(x+5)^2-2`

Add 2 to both sides

`0+2=(x+5)^2-2+2`

`=>2=(x+5)^2" "vec("swap round") " " (x+5)^2=2`

Square root both sides

`x+5=sqrt(2)`

Subtract 5 from both sides

`x=-5+-sqrt(2)`

`x~~-6.414` to 3 decimal places
`x~~-3.586` to 3 decimal places