How do you solve #-4x – 6y = -28# and #2x + 3y = 14 #?
1 Answer
Here's what I got.
Explanation:
Your starting system of two equations with two unknowns looks like this
#{(-4x - 6y = -28), (color(white)(..)2x + 3y = color(white)(-)14) :}#
Notice that if you multiply the second equation by
#2x + 3y = 14 " "| xx color(blue)((-2))#
#color(blue)((-2)) * 2x + color(blue)((-2)) * 3y = color(blue)((-2)) * 14#
#-4x -6y = -28#
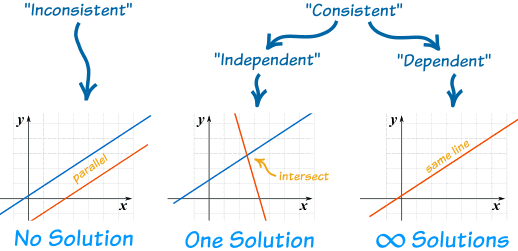
This means that your system of equations has an infinite number of solutions. This is the case because if you were to subtract this new form of the second equation from the first equation, you'd get
#{(-4x - 6y = -28" "| -), (-4x -6y = -28) :}#
#color(white)(aaaaaaa)/color(white)(aaaaaaaaaaaaaaaaa)#
#-4x - (-4x) - 6y - (-6y) = -28 - (-28)#
#-color(red)(cancel(color(black)(4x))) + color(red)(cancel(color(black)(4x))) - color(red)(cancel(color(black)(6y))) + color(red)(cancel(color(black)(6y))) = -color(red)(cancel(color(black)(28))) + color(red)(cancel(color(black)(28)))#
which of course gives
#0 = 0#
So, when does
In other words, you can plug in any value you want for
Alternatively, you can think about the two equations given to you as describing the same line. To check that this is the case, rearrange both equations in slope-intercept form
#-4x - 6y = -28#
#-6y = 4x -28 implies y = -2/3x + 14/3#
Similarly, you have
#2x + 3y = 14#
#3y = - 2x + 14 implies y= -2/3x + 14/3#
This once again leads to the conclusion that the system has an infinite number of solutions.