You can complete the square as a complete process, which is probably what they are looking for. Or you can do just part of this as a sort of cheat.
#color(blue)("Cheat method")#
Write as: #y=9(x^2-5/9x)-7#
#color(blue)(x_("vertex")=(-1/2)xx(-5/9) = +5/18)#
'...............................................................
Substitute #x=5/18# beck into the equation
#color(blue)(y_("vertex")=9(5/18)^2-5(5/18)-7=-7 25/36 =-277/36)#
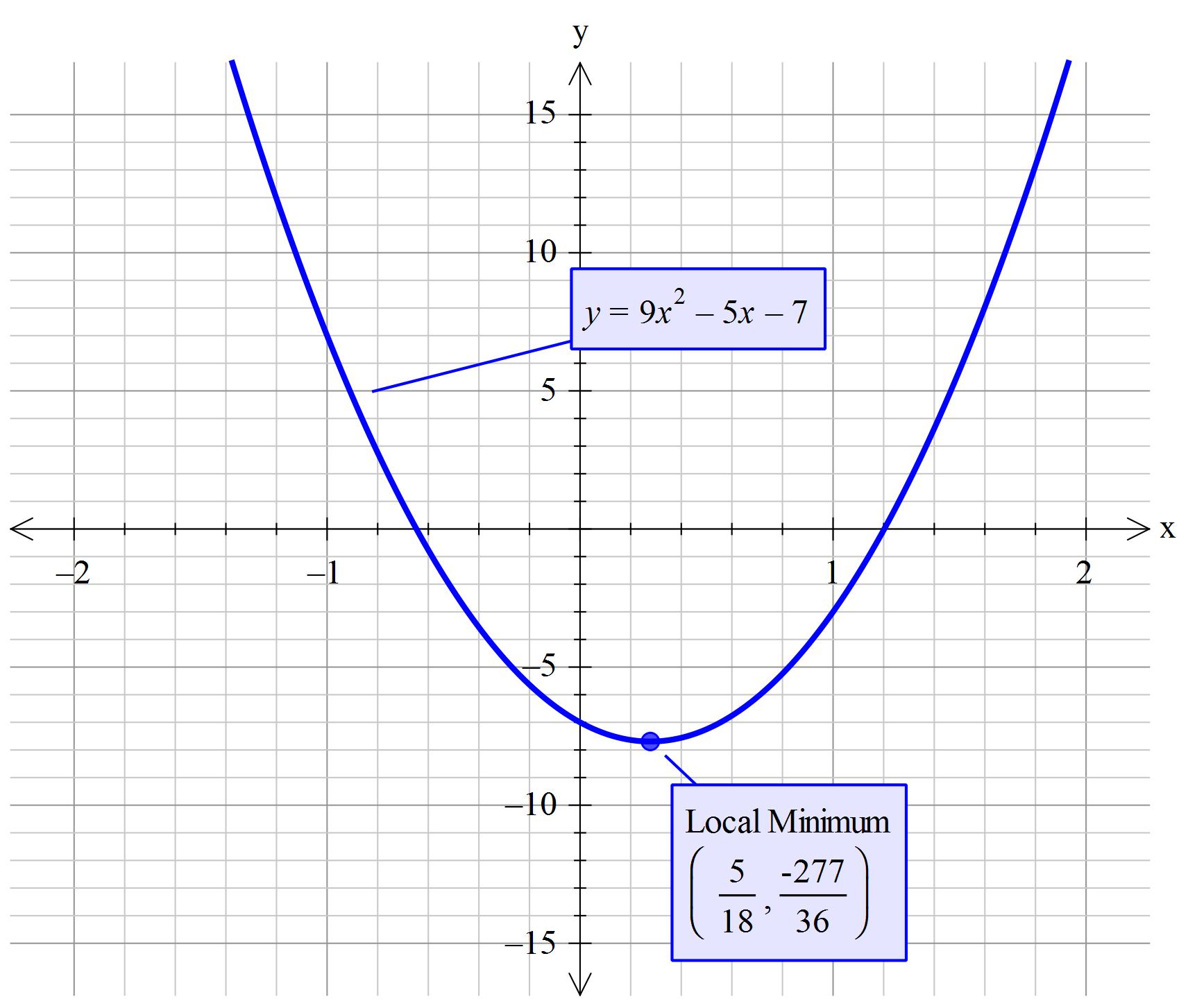
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Completing the square method")#
Write as: #y=9(x^2-5/9x)-7#
Halve the #-5/9# and add the corrective constant #k#
#y=9(x^2-5/18x)-7+k#
Remove the #x# from #-5/18x#
#y=9(x^2-5/18)-7+k#
Move the power of 2 to outside the brackets
#y=9(x-5/18)^2-7+k#............................Equation(1)
Now we compensate for the error we introduced by changing to this format.
#color(magenta)("The error comes from:" ->) y=color(magenta)9(x color(magenta)(-5/18))^(color(magenta)(2))-7+k#
so: #" "9xx(-5/18)^2+k=0" "larr" The correction"#
#25/36+k=0#
#=>k=-25/36#
Substitute for #k# in Equation(1)
#y=9(x-5/18)^2-7-25/36#
#y=9(x-5/18)^2color(green)(-277/36)#
#color(red)(x_("vertex")=(-1)xx(-5/18)=+5/18)#
#"Vertex" ->(x,y)=(color(red)(+5/18),color(green)(-277/36))#


