#"step-1 : draw the line "y=3/8 x+5 #
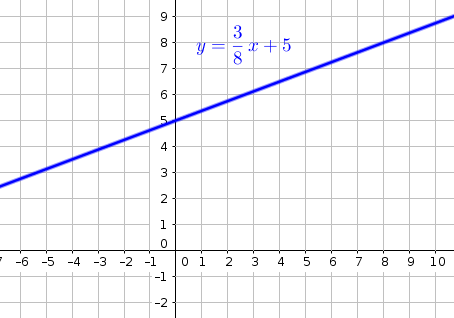
#"step-2 : locate "P_1 " and "P_2#
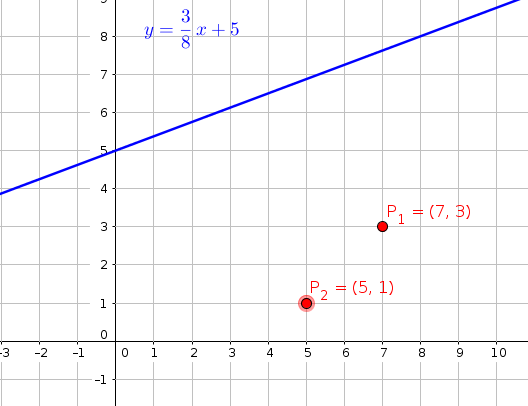
#"step -3 : draw a line segment between " P_1 and " P_2#
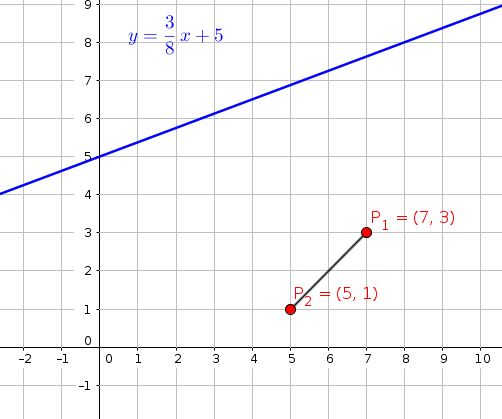
#"step-4 : find the middle point of line segment"#
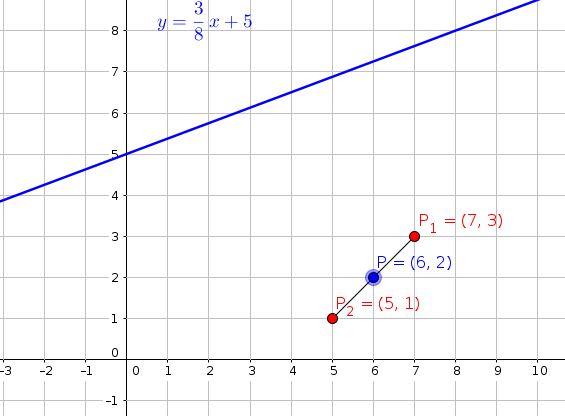
#P_x=(7+5)/2=6#
#P_y=(3+1)/2=2#
#P=(6,2)#
#"step-5 : draw a line perpendicular to line segment and passing through P"#
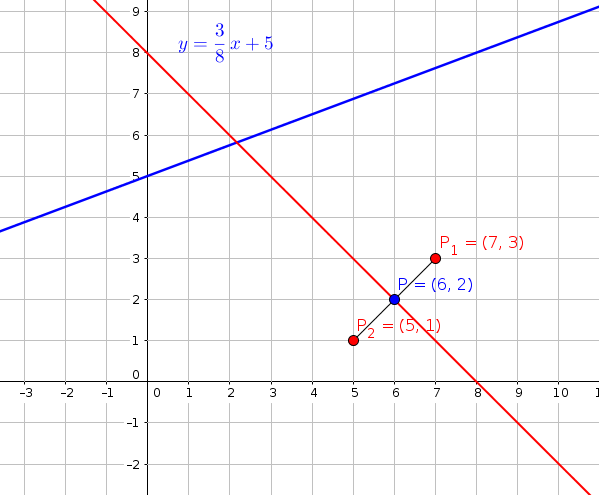
#"the red line's slope : "m_("red")#
#"segment's slope : "m_("segment")#
#m_("segment")*m_("red")=-1#
#1*m_("red")=-1#
#m_("red")=-1#
#y-2=-1(x-6)#
#y-2=-x+6#
#color(red)(y+x=8)" the red line equation"#
#"step-6 : now find the coordinate of center of circle (O)"#
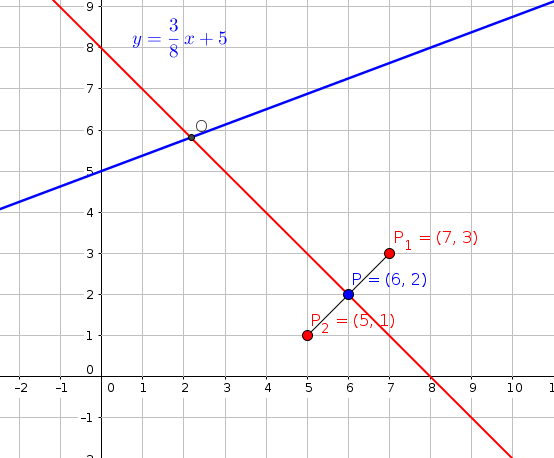
#"use the two equation :"#
#y=3/8 x+5#
#x+y=8#
#x+3/8 x+5=8#
#(11x)/8=8-5#
#11x=24#
#x=24/11=2.18#
#2.18+y=8#
#y=8-2.18=5.82#
#O=(2.18,5.82)#
#"step-7 : find distance between O and " P_1" (r)"#
#r^2=6-2.18)^2+(2-5.82)^2)#
#r^2=10.24+14.59=31.16#
#"step-8 : write equation"#
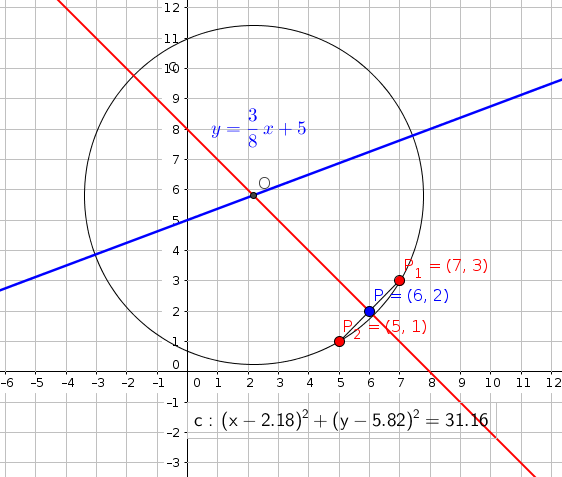
#(x-a)^2+(y-b)^2=r^2#
#(a,b)" center coordinates"#
#(x-2.18)^2+(y-5.82)^2=31.16#













