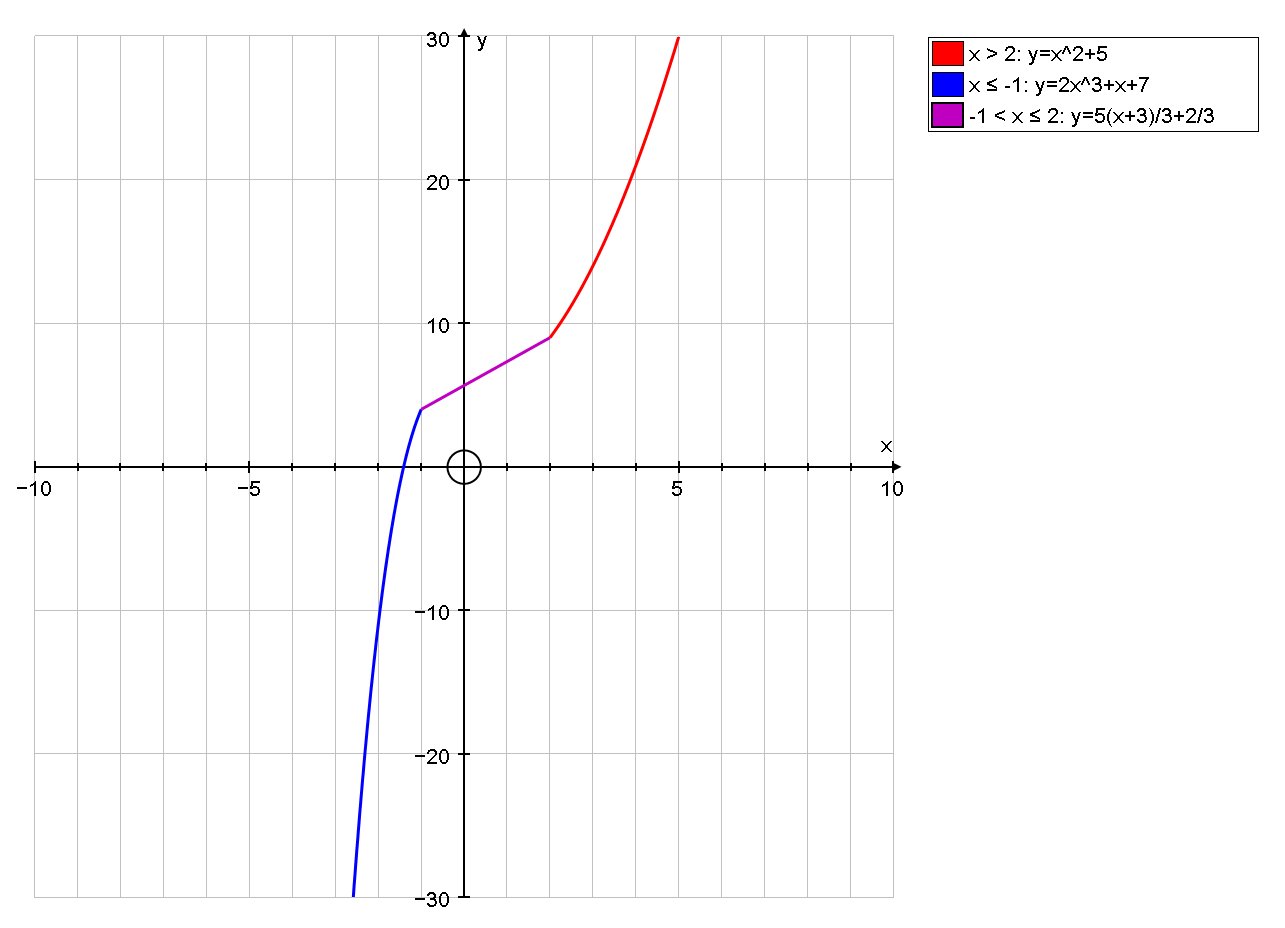
How do we find the values of k and m that makes function continue anywhere piecewise function of #(x^2) + 5# when x > 2, #m(x+3) + k# when #-1 < x <=2# and #2(x^3) + x + 7# when #x <=-1#?
2 Answers
Explanation:
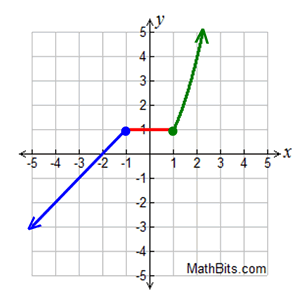
Here is an example of a continuous function.
Here is an example of a discontinuous function.
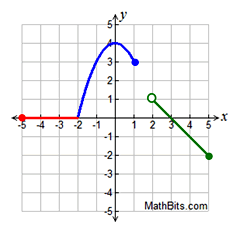
So, continuous functions are where everything is connected; there are no gaps or holes.
The y-value of
We need the graph of
The
We need the graph of
Hence, we can write a systems of equations with respect to
So, the function in the interval
Explanation:
We want to find
Just think about what we know so far, and how it would look:
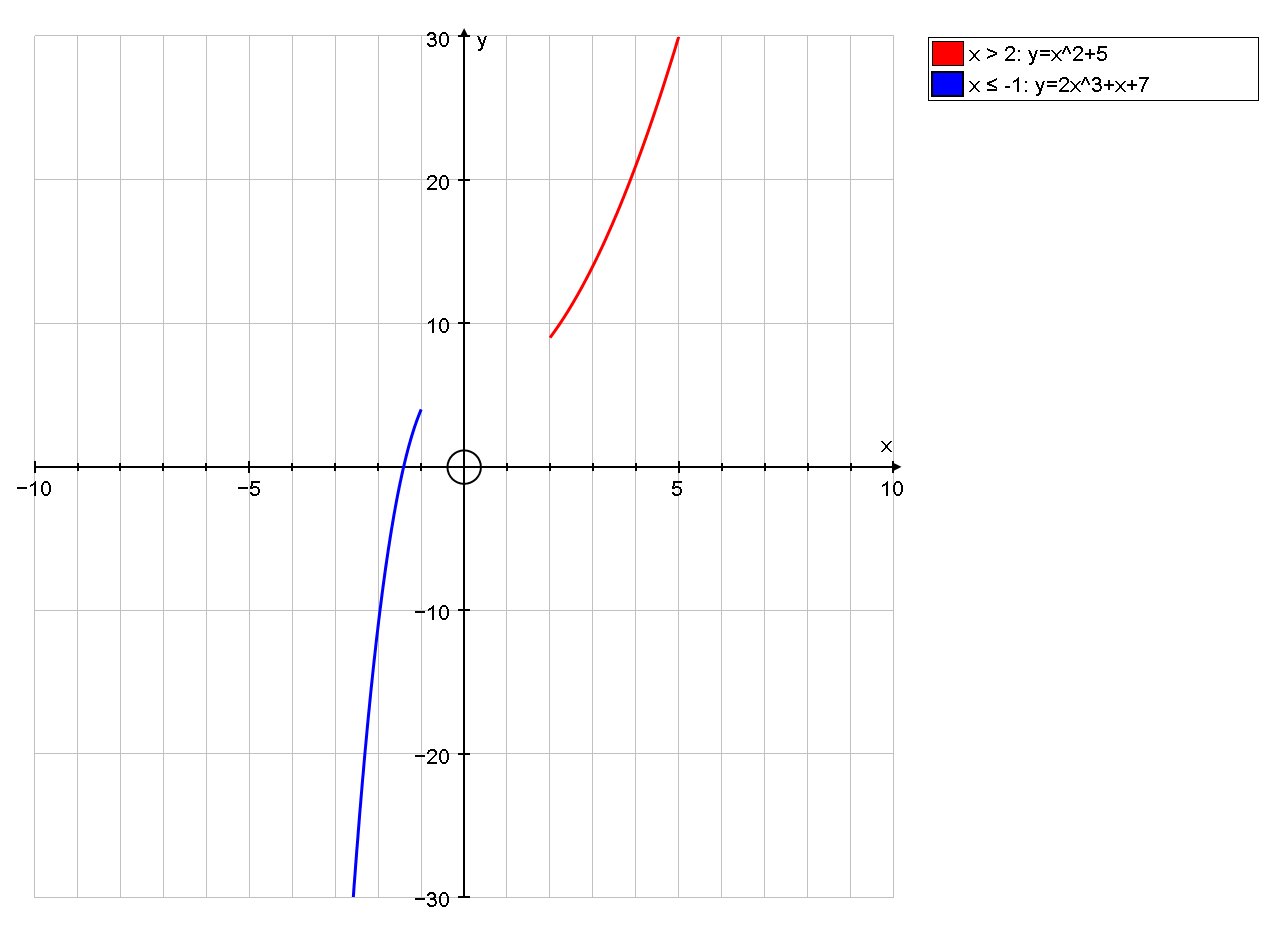
When
When
So for the mid interval we need a straight line whose equation is
This line would have the following gradient:
So our required line passes through
So the mid-section has equation
ie