What is the meaning and explanation of each equation? ( wave function, probability density, radial distribution function)

2 Answers
I was not going to answer because I am very rusty on this subject but nobody was answering so I tried...anyway take it with great caution!
Explanation:
If I remember correctly:
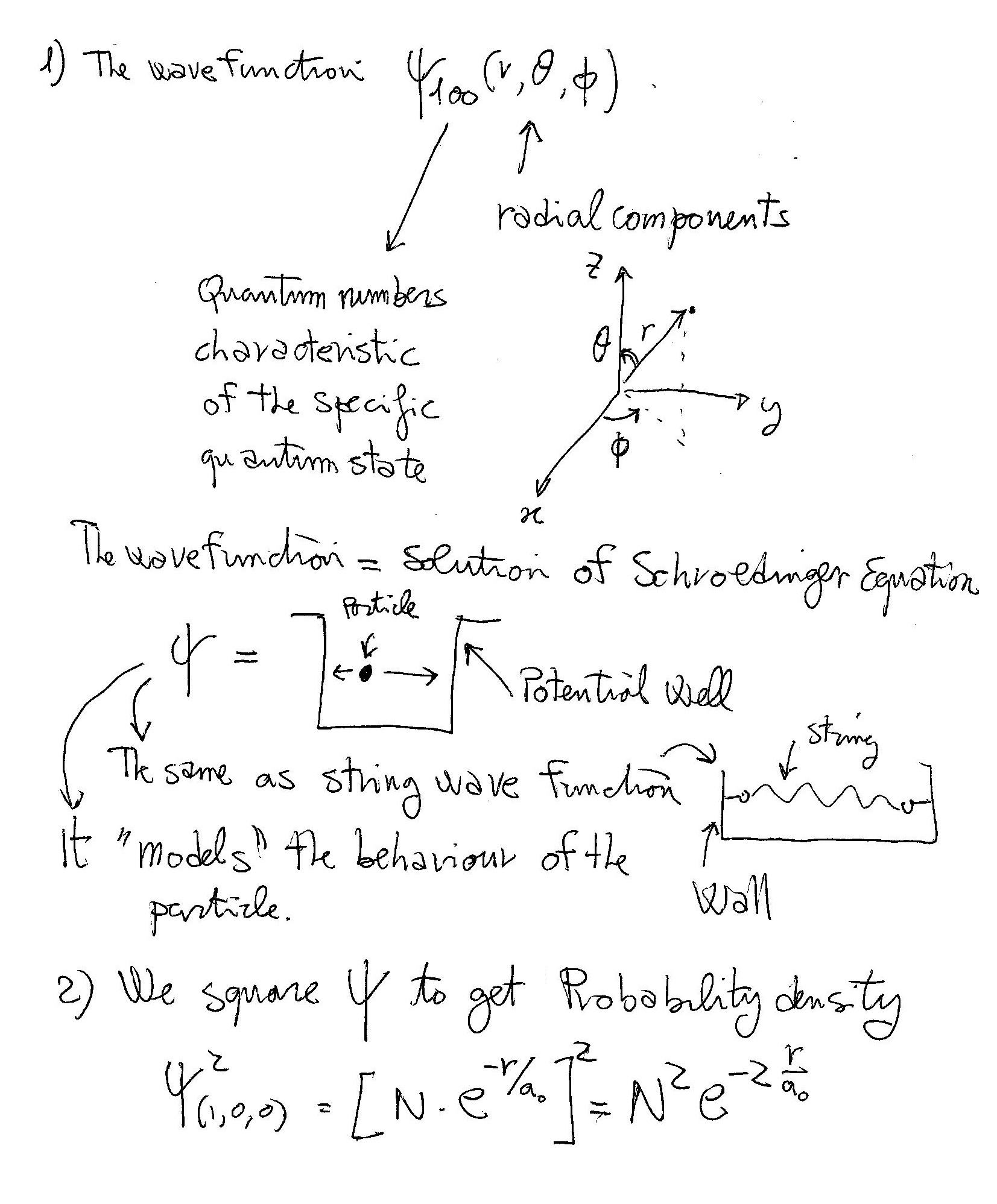

Schrödinger equation is a partial differential equation which describes how the quantum state of a quantum mechanical system changes with time.
Spherical coordinates are used to depict three dimensional space in terms of
For hydrogen atom the wave function of the Schrödinger equation can be written as product of three separate variables as
This gives us three equations. The equation for each of the three variables gives rise to a quantum number and the quantized energy states of the hydrogen atom. These can be found in terms of three spatial quantum numbers:
Since there is only one electron in the hydrogen atom, only Principal Quantum number
As such the wave function representing the ground state electron reduces to
where
We need to remember that
- The magnitude of the wave function at a particular location in space is proportional to the amplitude of the wave at that point. This has been explained above.
- The square of the wave function at any given point is proportional to the probability of finding an electron at that point, which leads to a probability distribution of locating an electron in space. As shown below it is square of the wave function
#Psi_(1,0,0)^2(r,theta, φ)=N^2e^(-(2r)/a_0)#
It is interesting to note that probability of finding the electron at
In practice we need to normalize the probability by integrating the expression over the complete space and equate it to
As mentioned in 2. above we can calculate the radial probability distribution of locating the electron on all points situated on the surface of sphere of radius
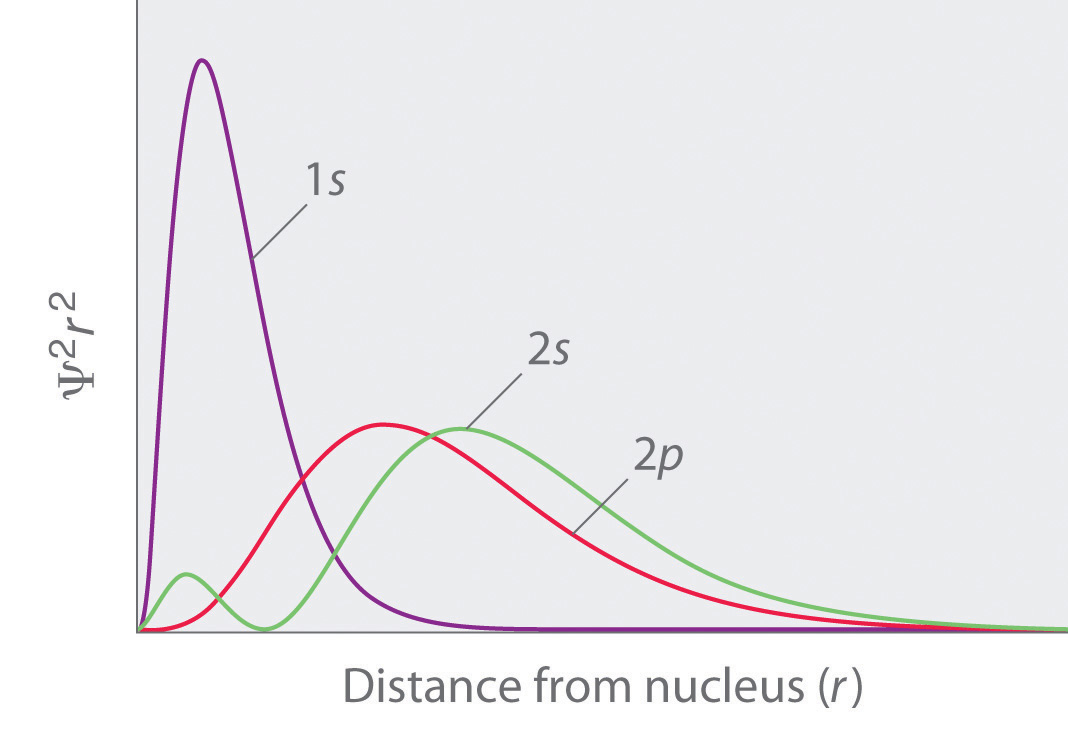
This is plotted as in the figure above. See 1s probability. Please note that

