Question

How do you solve the inequality `(x-1)(x+4)(x-3)>0`?

Answer 1

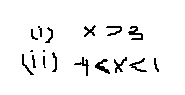
Explanation:

There can be three situations for the inequality to hold good:

I.All terms are positive that means `x>1, x> -4 and x>3`. This simply means that x>3

II `x-1>0 , x+4 <0 and x-3<0`. This means x>1, but x< -4 and x<3, that is x>1 and x<-4 ( if x< -4, it would automatically be less than 3)

III`x+4>0, x-1<0 and x-3<0`. This means x>-4, x<1 and x<3. This implies that x>-4 and x<1 (if x<1, it would automatically be less than 3)

IV `x+3>0, x-1<0 and x+4<0`. This would mean x> -3, x<1 and x<-4. This implies that x> -3 and x<-4 (if x<-4, it would automatically be less than 1)

Analyzing the above options, it would be clear that II is not possible, because x cannot be greater than 1 and less than -4 at the same time.
Like wise IV is also not possible because x can not be greater than -3 and less than -4 at the same time

Hence I and III are the only solutions for the Inequality.