Question

How do you write the equation of the hyperbola given Foci: (0,-9),(0,9) and vertices (0,-3sqrt5), (0,3sqrt5)?

Answer 1

Because it is the y coordinate that is changing for the given points, use the vertical transverse axis form:
`(y-k)^2/a^2-(x-h)^2/b^2=1" [1]"`
vertices: `(h,k+-a)`
foci: `(h,k+-sqrt(a^2+b^2))`

Explanation:

Using the given points, write the following equations:

`h = 0" [2]"`
`k - a = -3sqrt5" [3]"`
`k + a = 3sqrt5" [4]"`
`k - sqrt(a^2 + b^2) = -9" [5]"`
`k + sqrt(a^2 + b^2) = 9" [6]"`

To obtain the value of k, add equations [3] and [4]:

`2k = 0`

`k = 0`

To obtain the value of a, substitute 0 for k into equation [4]:

`a = 3sqrt5`

Substitute the known values of "k" and "a" into equation 6 and solve for b:

`0 + sqrt((3sqrt5)^2 + b^2) = 9`

`b^2 + 45 = 81`

`b^2 = 36`

`b = 6`

Substitute the known values into equation [1]:

`(y-0)^2/(3sqrt5)^2-(x-0)^2/6^2=1" [7]"`

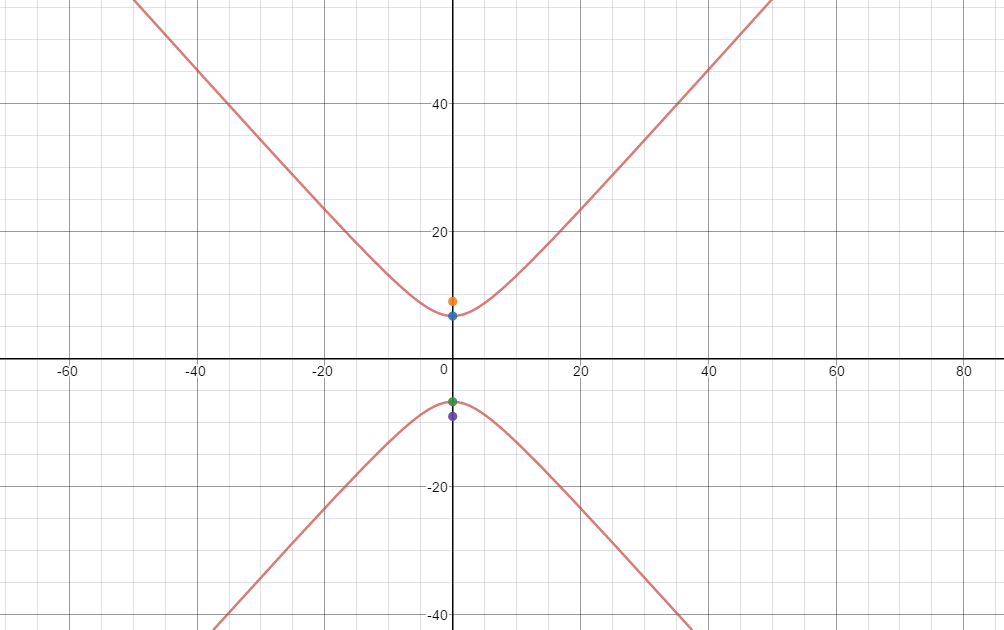
Here is a graph of equation [7] with vertices and foci: