Question

How do you find two unit vectors that are orthogonal to (-3,4)?

Answer 1

I got:

`color(blue)(hatv = << 4/5,3/5,0 >>)`
`color(blue)(hatw = << 0,0,-1 >>)`

assuming that the vectors all have to be orthogonal to each other (so the two vectors we found are orthogonal to each other as well).

Note that we could have also used any of the following pairs:

`color(blue)(hatv = << -4/5,-3/5,0 >>)`
`color(blue)(hatw = << 0,0,-1 >>)`

`color(blue)(hatv = << 4/5,3/5,0 >>)`
`color(blue)(hatw = << 0,0,1 >>)`

`color(blue)(hatv = << -4/5,-3/5,0 >>)`
`color(blue)(hatw = << 0,0,1 >>)`

Try drawing these out and see if you can see where I'm getting this.

---

Orthogonal means `90^@` from another vector, and unit vectors have a length of `1`.

THE FIRST VECTOR

One way to generate the first vector orthogonal to `<< -3,4 >>` is to use a rotation matrix to rotate the original vector by `90^@`.

For a clockwise rotation of `theta` degrees:

`hatR = [(costheta,sintheta),(-sintheta,costheta)]`

Plug in `theta = 90^@` so that we get:

`hatR = [(cos90^@,sin90^@),(-sin90^@,cos90^@)]`

`= [(0,1),(-1,0)]`

So:

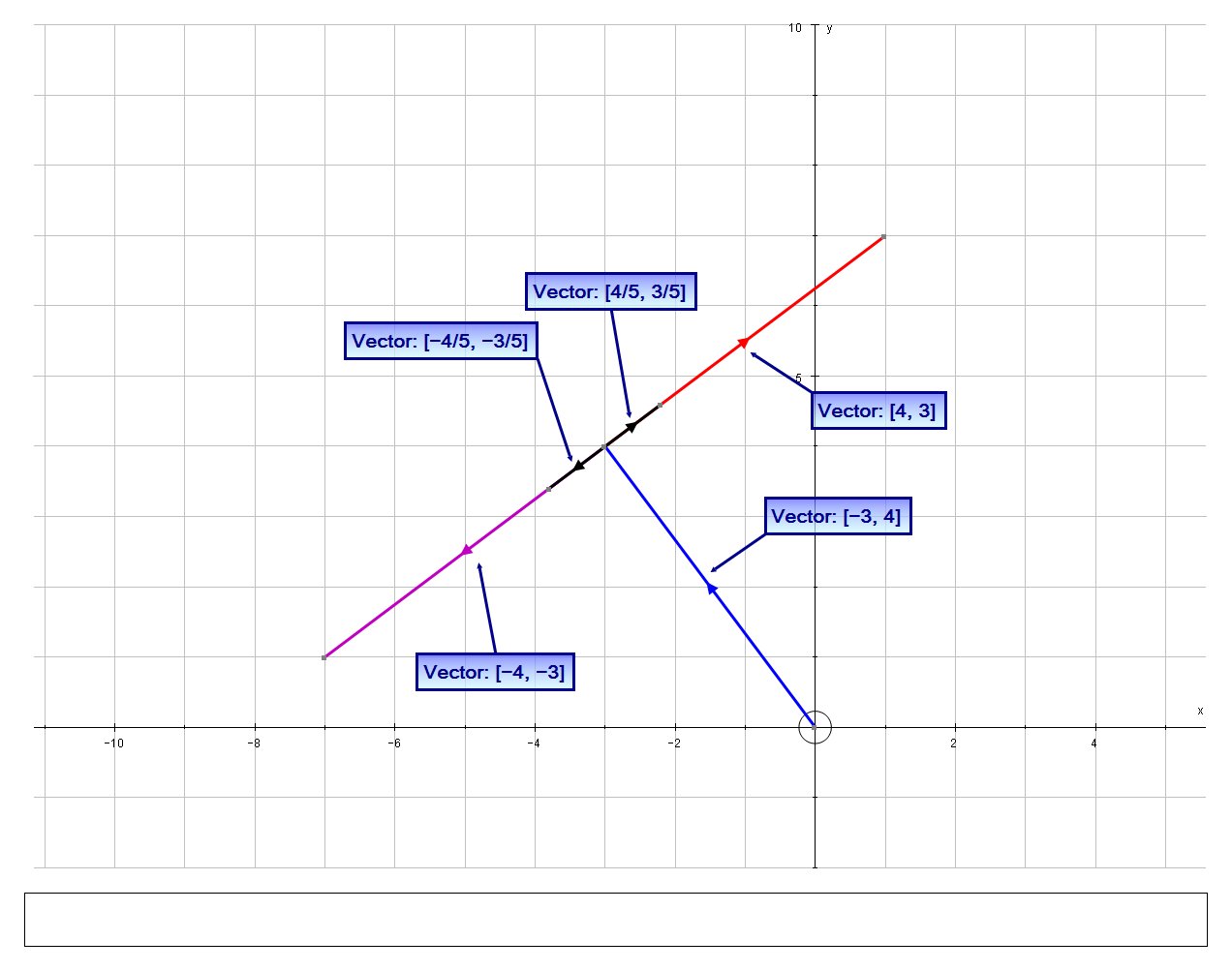
`hatR[(3),(4)]`

`= [(0,1),(-1,0)][(-3),(4)]`

`= << 4,3 >>`

And you can see that they are orthogonal by checking the dot product:

`<< -3, 4 >> cdot << 4, 3 >>`

`= -3*4 + 4*3 = -12 + 12 = 0` `color(blue)(sqrt"")`

You can also check by drawing out the actual vector on the xy-plane.

THE SECOND VECTOR

The second vector orthogonal to these can be found from taking the cross product of the two vectors we now have. Try converting the vectors to a sum of unit vectors `hati` and `hatj` multiplied by coefficients:

`<< -3, 4 >> = -3hati + 4hatj`

`<< 4, 3 >> = 4hati + 3hatj`

Their cross product is then:

`(-3hati + 4hatj)xx(4hati + 3hatj)`

`= -12cancel(hatixxhati)^(0) - 9hatixxhatj + 16hatjxxhati + 12cancel(hatjxxhatj)^(0)`

`= -9hatk - 16hatixxhatj`

`= -9hatk - 16hatk`

`= -25hatk`

`= << 0,0,-25 >>`

where we use the identities `hatixxhatj = hatk` and `hatixxhatj = -hatjxxhati`.

Then, the two vectors we evaluated before must be projected onto three dimensions. Let us set them on the `xy`-plane so that our vectors are:

`<< -3,4,0 >>`
`color(green)(<< 4,3,0 >>)`
`color(green)(<< 0,0,-25 >>)`

TURNING THE VECTORS INTO "UNIT VECTORS"

The two vectors we found were not unit vectors though, and are just vectors. So, we just have to normalize them now:

`hatv = (<< 4,3,0 >>)/(|| << 4,3,0 >> ||)`

`= (<< 4,3,0 >>)/(sqrt(4^2 + 3^2 + 0^2))`

`= (<< 4,3,0 >>)/5`

`= << 4/5,3/5,0 >>`

Similarly, for the other one:

`hatw = (<< 0,0,-25 >>)/(||<< 0,0,-25 >>||)`

`= (<< 0,0,-25 >>)/25`

`= << 0,0,-1 >>`

So, the two unit vectors orthogonal to `<< -3,4,0 >>` are:

`color(blue)(hatv = << 4/5,3/5,0 >>)`
`color(blue)(hatw = << 0,0,-1 >>)`

NOTE: If you continue to normalize the original provided vector to get `hatu = << -3/5,4/5, 0 >>`, you can show that `hatu xx hatv = hatw`, `hatv xx hatw = hatu`, `hatw xx hatu = hatv`, and so on, just like the unit vectors `hati,hatj,hatk`. That would show that they are orthogonal and unit vectors.

Answer 2

The unit vectors are:

`<< 4/5, 3/5>>` and `<< -4/5, -3/5>>`

Explanation:

Suppose a suitable orthogonal vector in `RR^2` is denoted by:

`<< a, b>>`

If this vector is orthogonal to `<< -3,4 >>` then their dot product will be zero; that is:

`<< a, b>> * << -3,4 >> = 0`

`:. -3a+4b = 0`

We now need to find suitable values of `a` and `b` satisfying this relationship (note we have one equation and two unknowns):

Arbitrarily choose `a=4`

`:. -12+4b = 0 =>. b=3`

Arbitrarily choose `a=-4`

`:. 12+4b = 0 =>. b=-3`

Hence two orthogonal vectors are:

`<< 4, 3>>` and `<< -4, -3>>`

We now need to normalise the vectors (as the question asked for unit vectors):

In both cases:

`|<< 4, 3>>| = |<< -4, -3>>| = sqrt(16+9) = 5`

We can normalise the vectors by multiplying by `1/5`

Hence, the unit vectors are:

`<< 4/5, 3/5>>` and `<< -4/5, -3/5>>`