Question

How do you integrate `int 1/(x^3sqrt(9-x^2))dx` using trigonometric substitution?

Answer 1

`-1/54(ln|(3 + sqrt(9 - x^2))/x| + (3sqrt(9 - x^2))/x^2) + C`

Explanation:

Whenever you have an integral with a `√` of the form `sqrt(a^2 - x^2)`, use the substitution `x = asintheta`.

So, let `x = 3sintheta`. Then `dx= 3costhetad theta`.

`=>int 1/((3sintheta)^3sqrt(9 - (3sintheta)^2)) * 3costhetad theta`

`=>int 1/(27sin^3theta sqrt(9 - 9sin^2theta)) * 3costheta d theta`

`=>int 1/(27sin^3thetasqrt(9(1 - sin^2theta))) * 3costheta d theta`

`=>int 1/(27sin^3thetasqrt(9cos^2theta)) * 3costheta d theta`

`=>int 1/(27sin^3theta3costheta) * 3costheta d theta`

`=>int 1/(27sin^3theta) d theta`

`=>1/27int csc^3theta d theta`

This can be integrated as `-(ln|csctheta + cottheta| + cotthetacsctheta)/2 + C`. This is derived using integration by parts. You can see the full proof here.

`=>-1/54(ln|csctheta + cottheta| + cotthetacsctheta) + C`

Now draw a triangle to determine expressions for cosecant and cotangent.

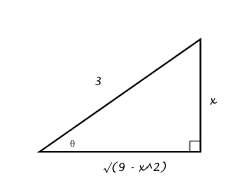
`=>-1/54(ln|(3 + sqrt(9 - x^2))/x| + (3sqrt(9 - x^2))/x^2) + C`

Hopefully this helps!