A triangle has sides A, B, and C. The angle between sides A and B is #(5pi)/12# and the angle between sides B and C is #pi/12#. If side B has a length of 12, what is the area of the triangle?

Question

1280 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-02-02T03:55:27

Area = 18 units

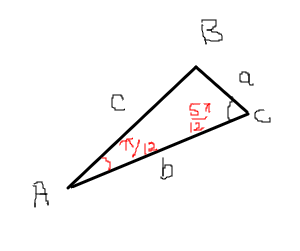
enter image source here

The given triangle is sketched as in the figure above. Angle B would be # pi -pi/12 -(5pi)/12 = pi/2#

Side b is 12. It is the hypotenuse because it is opposite the right angle B.

For area, base and altitude is required. In this case it is side 'a' and side 'c'.

Side 'c' = #12 cos (pi/12)#

Side 'a' = # 12 sin (pi/12)#

Area = #1/2 (12 sin (pi/12) *12 cos (pi/12))#
=#72 sin (pi/12) cos (pi/12)# =# 36 (2sin (pi/12) cos (pi/12))#= 36 sin pi/6= 36#1/2#= 18

Area = 18 units.