Question

How do you find the vertex and the intercepts for `y= -x^2 + 9`?

Answer 1

Vertex: `(0,9)`
Y-intercept: `y=9`
X-intercepts: `x=-3 and x=+3`

Explanation:

Remember the standard vertex form for a parabola is
`color(white)("XXX")y=color(green)m(x-color(red)a)^2+color(blue)b`
with vertex at `(color(red)a,color(blue)b)`

Re-writing the given equation: `y=-x^2+9`
into explicit standard vertex form:
`color(white)("XXX")y=color(green)(-1)(x-color(red)0)^2+color(blue)9`
with vertex at `(color(red)0,color(blue)9)`

The Y-intercept is the value of `y` when `x=color(magenta)0`
`color(white)("XXX")y=-color(magenta)0^2+9=9`

The X-intercepts are the values of `x` possible when `y=color(orange)0`
`color(white)("XXX")color(orange)0=-x^2+9`
`color(white)("XXX")rarr x^2=9`
`color(white)("XXX")rarr x=+-3`

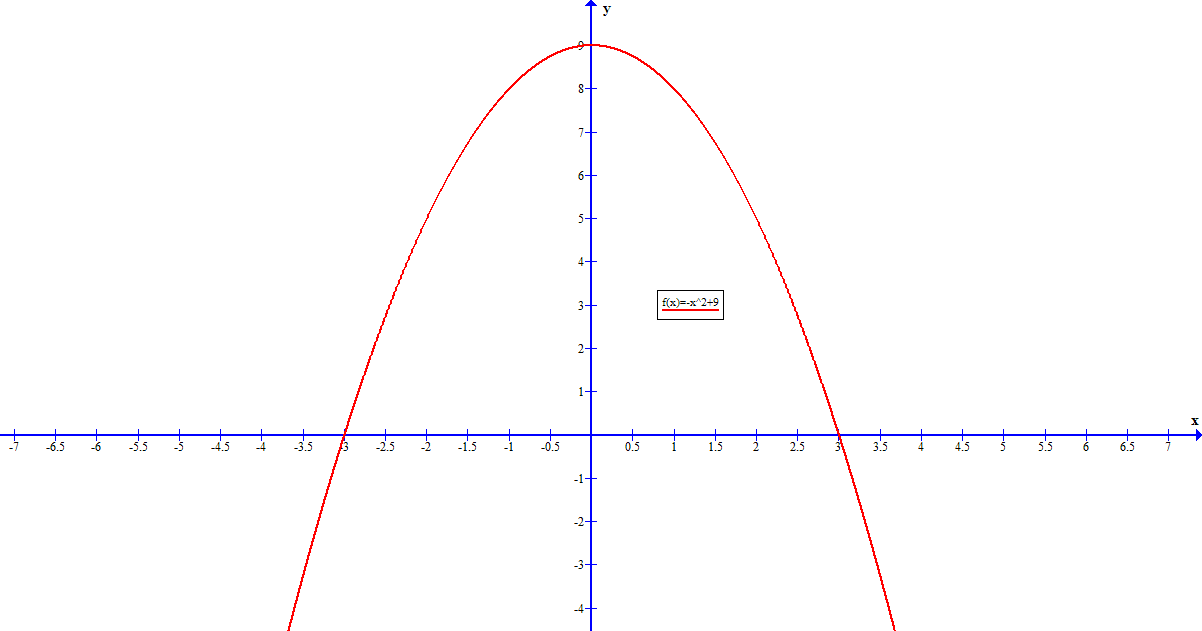
Here is the graph for verification purposes: