Question

How do you write a quadratic function in vertex form whose has vertex (-3,-2) and passes through point (1,14)?

Answer 1

`y=(x+3)^2-2`

Explanation:

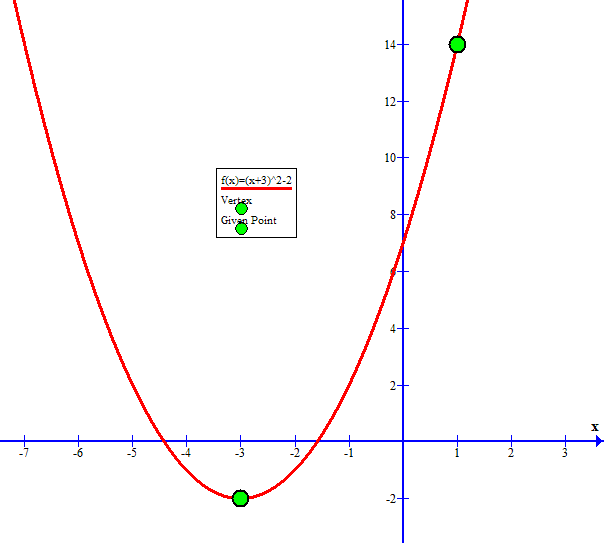
Any quadratic function with vertex at `(color(red)(-3),color(blue)(-2))`
can be written in the form:
`color(white)("XXX")y=color(green)m(x-color(red)(""(-3)))^2+color(blue)(""(-2))` for some constant `color(green)m`
or (simplified)
`color(white)("XXX")y=color(green)m(x+3)^2-2`

If `(color(magenta)x,color(brown)y)=(color(magenta)1,color(brown)(14))` is a solution for some specific quadratic with this form:
`color(white)("XXX")color(brown)(14) =color(green)m(color(magenta)1+3)^2-2`

`rarrcolor(white)("XXX")14=16color(green)m-2`

`rarrcolor(white)("XXX")16color(green)m=16`

`rarrcolor(white)("XXX")color(green)m=1`

Given the complete quadratic equation:
`color(white)("XXX")y=color(green)1(x+3)^2-2`

As verification here is the graph of `y=(x+3)^2-2`