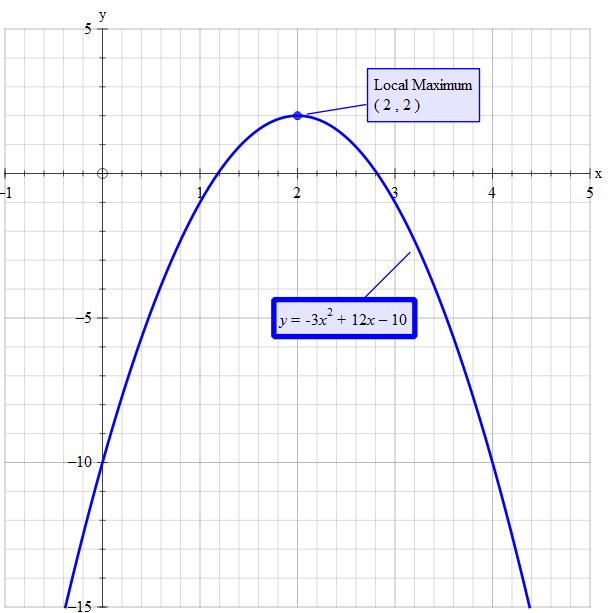
How do you find the vertex of #y= -3x^2+ 12x-10#?
2 Answers
Vertex:
Explanation:
Use completing of the squares to put the equation in standard form:
-
Factor the
#x# terms:#y = -3(x^2 - 4x) -10# -
Take
#1/2# of the#x-# term coefficient:#1/2 * -4 = -2# :
#(x-2)^2# is the completed square. -
Square the value from step 2:
#(-2)^2 = 4# -
Multiply the value from step 3 by the factored value
#-3# :#4*-3 = -12# . This means we need to add#12# to the equation because when we completed the square we subtracted#-12# :# -3(x -2)^2 = -3(x^2 - 4x +4) = -3x^2 +12x -12# -
#y = -3(x -2)^2 - 10 +12# -
#y = -3(x -2)^2 + 2# -
vertex:
#(2, 2)#
There is a sort of cheat (not really) way of doing this
Vertex
Explanation:
Write as
This part way to completing the square.
Determine y by substitution
Vertex