A triangle has two corners with angles of # (2 pi ) / 3 # and # ( pi )/ 6 #. If one side of the triangle has a length of #1 #, what is the largest possible area of the triangle?
2 Answers
I got an area of (approximately)
Explanation:
If two of the angles are
If one of its sides has a length of
Suppose the long side has a length of
By the Law of Sines
We have a triangle with sides with lengths
The semiperimeter,
and
Using Heron's Formula for the area of a triangle:
Maximum area:
Explanation:
All solutions rely on recognizing that the third angle must be
There are two possible configurations to consider.
For brevity, you might want to skip to version 2 which has the larger area.
In Version 1, the side with length
In Version 2, the side with length
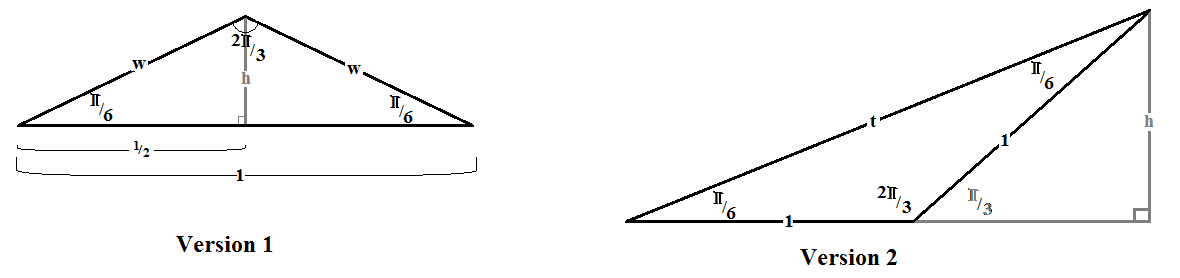
Version 1
Solution 1: Determine the area using side with length 1 as the base and a calculated height.
By definition of the
The angle
So
and
This gives an approximate area of
Solution 2: Determine the length of the missing sides and use Heron's Formula
perimeter is
and
semiperimeter,
By Heron's Formula
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Version 2
Solution 1: Determine the area using one of the sides with length 1 as the base and a calculated height
By definition of the
Note that
So Version 2 gives the larger area and thus is the version being asked for.
Solution 2: Determine the length of the missing side (using Law of Sines) and apply Heron's Formula.
(highlights only)
missing side:
semiperimeter
