Question

A triangle has sides A, B, and C. The angle between sides A and B is `pi/3`. If side C has a length of `4` and the angle between sides B and C is `pi/12`, what is the length of side A?

Answer 1

`A = 1.1954...`

Explanation:

The triangle described looks like this (not to scale):

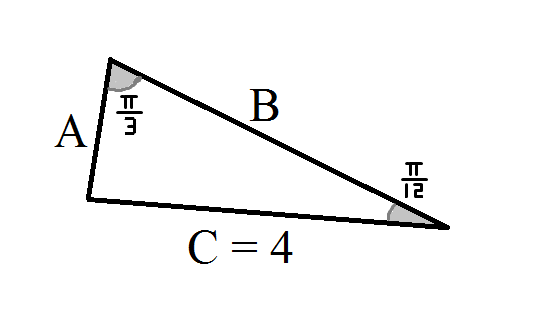
For any triangle as shown below, where `a` and `A` represent a side and its opposite angle, respectively, the law of Sines states that:

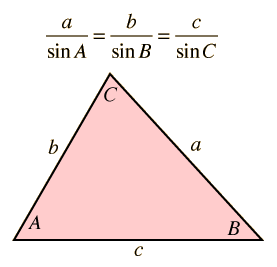
Therefore, by the law of Sines:

`A/(sin(pi/12))= C/(sin(pi/3)`

`A/(sin(pi/12)) = 4/(sin(pi/3))`

`A = (4sin(pi/12))/(sin(pi/3)) = 1.1954...`

Final Answer