A circle has a center that falls on the line #y = 7/9x +7 # and passes through # ( 2 ,3 )# and #(5 ,1 )#. What is the equation of the circle?
1 Answer
(I apologize for the very lengthy solution; I tried to do every step in detail.)
Explanation:
By definition, connecting the points (2,3) and (5,1) must form a chord on the circle.
As illustrated below, the Perpendicular Bisector of a Chord theorem states that for any chord on a circle, the perpendicular bisector of that chord will pass through the center of the circle.
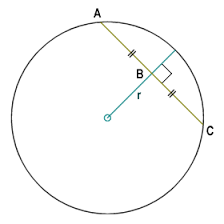
Therefore, the center of the circle we are trying to find must lie along the perpendicular bisector of the segment formed by connecting (2,3) and (5,1). So, let's write an equation for this line. To do this, we need to find the slope of the bisector, and a point on the bisector.
A point on the perpendicular bisector can be found with the midpoint equation:
#(color(orange)((x_1+x_2)/2), color(limegreen)((y_1+y_2)/2)) = (color(orange)((2+5)/2), color(limegreen)((3+1)/2)) = (color(orange)3.5, color(limegreen)2)# The slope of the bisector is perpendicular to the slope of the line formed by (2,3) and (5,1). Using
#m# for slope, we can find the bisector's slope with:
#color(red)(m_("bisector")) = (-1)/(m_("chord")) = (-1)/((3-1)/(2-5)) = (-1)/(-2/3) = color(red)(3/2)#
Now, we can use point-slope form to write and simplify the equation for the bisector:
#y - color(limegreen)2 = color(red)(3/2)(x - color(orange)3.5)#
#y - 2 = 3/2x - 21/4#
#color(white)"xxx-" y = 3/2x-13/4#
So, we know that the center must be on this line. But, it must also be on the line
#y = 7/9x+7#
#y = 3/2x-13/4#
#7/9x+7 = 3/2x-13/4#
#41/4 = 13/18x#
#color(orange)14.192 = x#
#therefore y = 3/2(color(orange)14.192)-13/4 = color(limegreen)18.038#
Now, we know that the center of the circle is
#r^2 = (color(orange)14.192-2)^2 + (color(limegreen)18.038-3)^2 = color(blue)374.786#
Therefore, the equation for the circle is:
#(x - color(orange)14.192)^2+(y - color(limegreen)18.038)^2 = color(blue)374.786#
Final Answer

