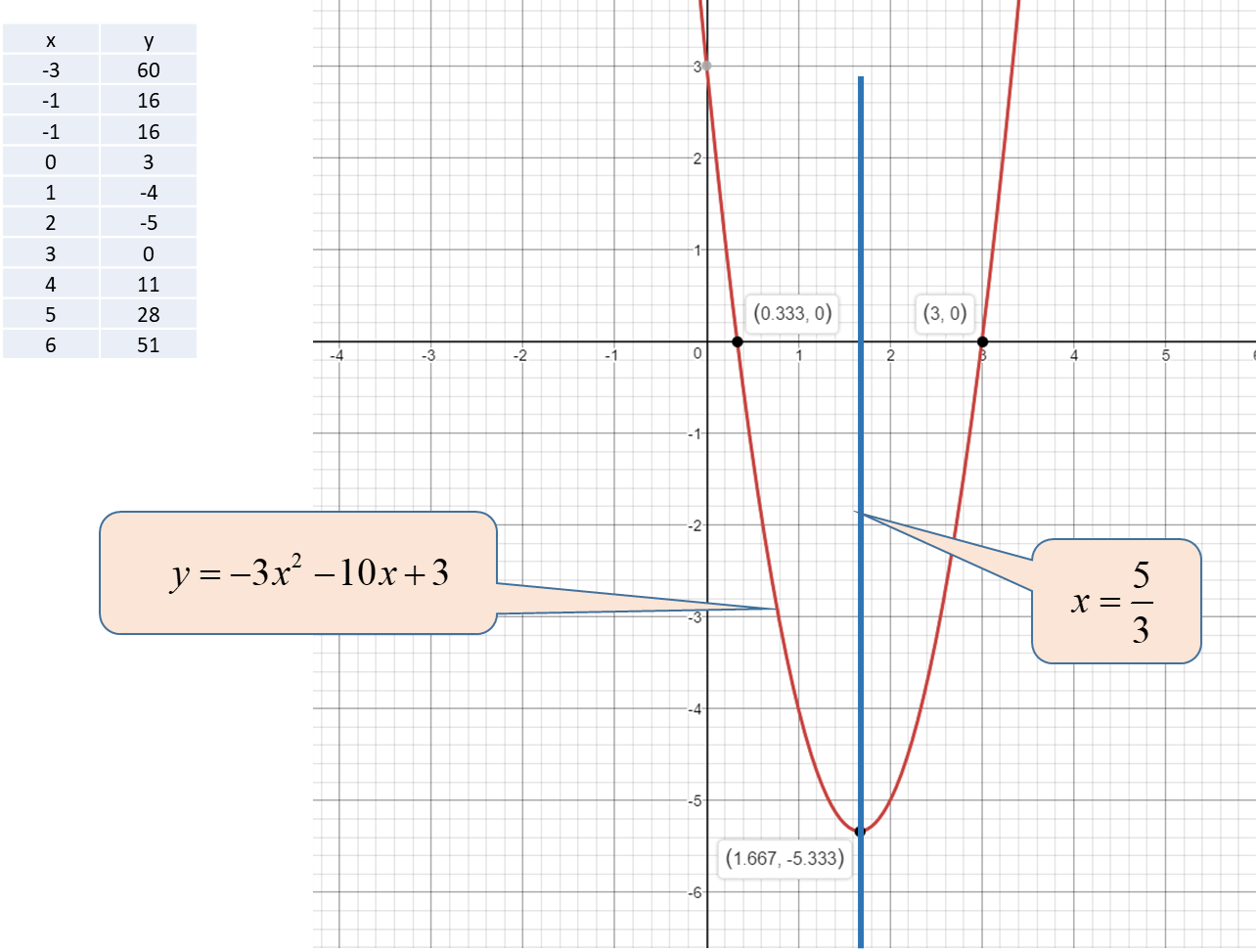
How do you graph, label the vertex, axis of symmetry and x intercepts of y=(3x-1)(x-3)?
2 Answers
graph{(3x-1)(x-3) [-20, 20, -10, 10]}
Vertex = (
Axis of symmetry =
X-intercepts =
Explanation:
Multiplying the two brackets we get the quadratic,
Comparing with
and the Discriminant =
Co-ordinates of Vertex of parabola are (
plug the the values of
Axis of symmetry is the x-coordinate of Vertex i.e
x-intercept of the parabola is basically the roots of equation.
Roots can be obtained by equating the function to
either
this gives
These are the x-intercepts.
X-intercept
x=1/3
x=3
Vertex(5/3, -16/3)
Axis of symmetryx=5/3
Explanation:
Given -
y=(3x-1)(x-3)
X-intercept
At
(3x-1)(x-3)=0
3x=1
x=1/3
x=3
y=3x^2-x-9x+3
y=3x^2-10x+3
Vertex
x=(-b)/(2a)=(-(-10))/(2 xx3)=10/6=5/3
At
y=3(5/3)^2-10(5/3)+3
y=3(25/9)-50/3+3
y=25/3-50/3+3
y=(25-50+9)/3=-16/3
Vertex
Axis of symmetry