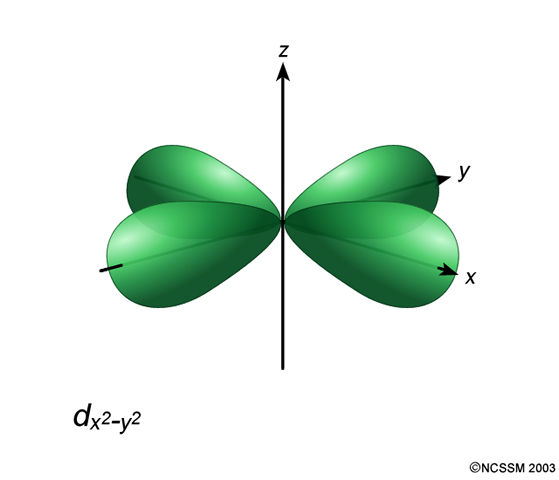
Significance? Well, it corresponds to one of the magnetic quantum numbers in the set m_l = {-2, -1, 0, +1, +2}, and has m_l = -2 by convention.
The 3d_(x^2 - y^2) orbital is the one lying along the axes:
COMMON BONDING CASES
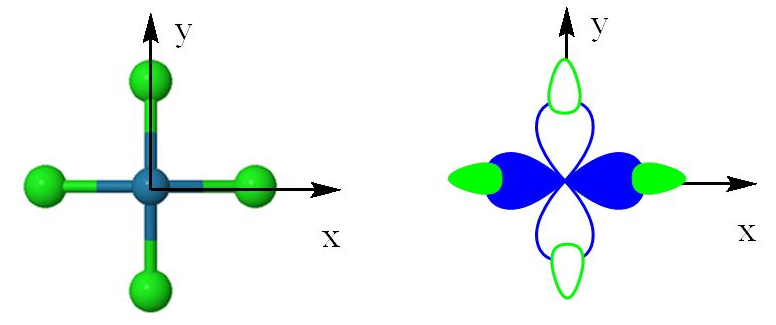
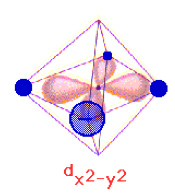
Because of that, it is often used to sigma (sigma) bond with surrounding ligands, particularly in a transition metal complex. You'll see a strong contribution from this orbital most often in...
square planar complexes:
and octahedral complexes:
ENERGIES
In an atom, it is degenerate with the other "four" 3d orbitals, the d_(z^2), d_(xy), d_(xz), and d_(yz).
In a complex, the d orbitals split in accordance with their symmetry (horizontal correspondence) and energy (vertical separations) with respect to the other d orbitals:
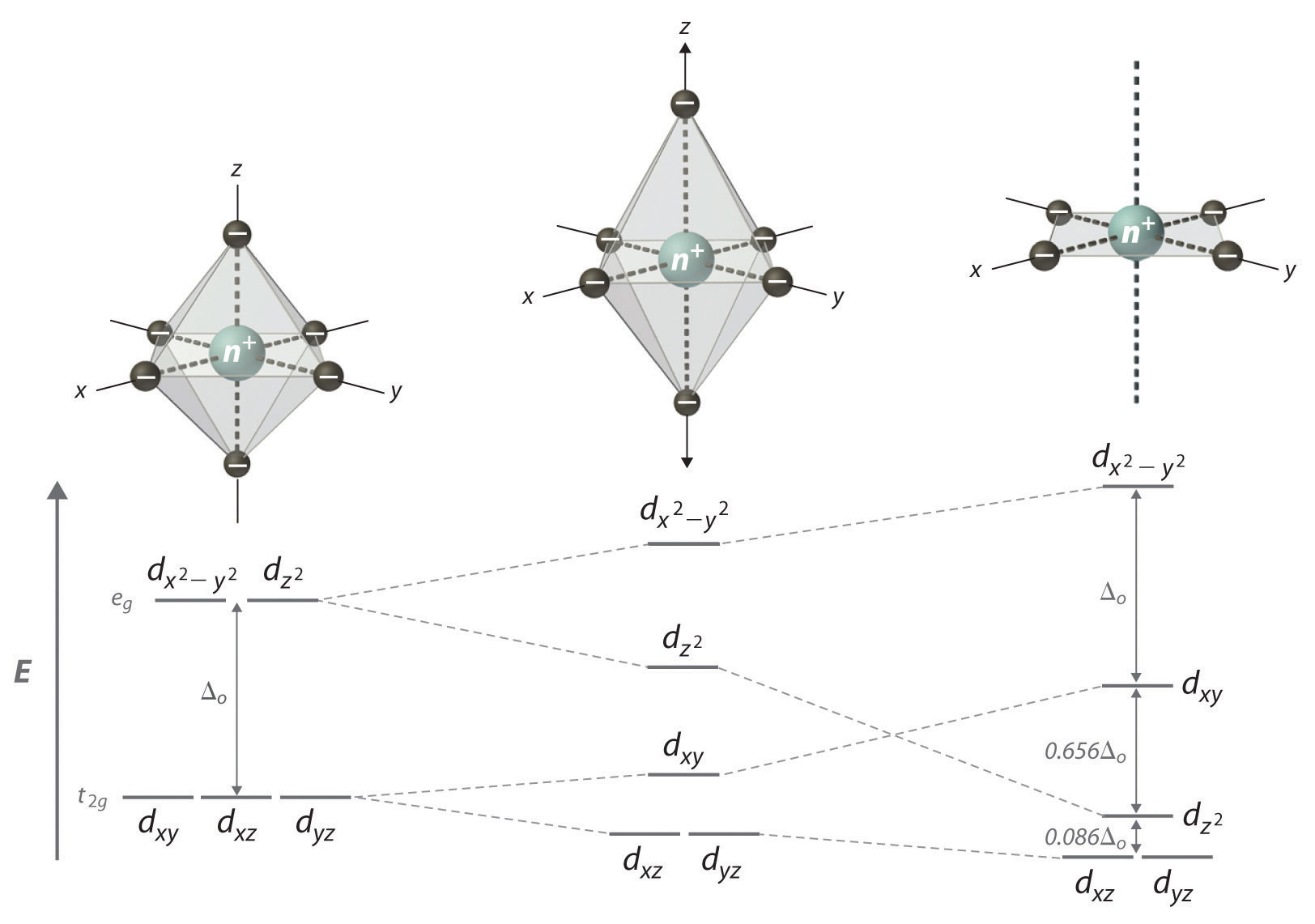
(For the octahedral complex, the symmetries from top to bottom were E_g and T_(2g), and for the square planar complex, the symmetries from top to bottom are B_(1g), B_(2g), A_(1g), and E_g.)





