Two corners of a triangle have angles of # ( pi )/ 3 # and # ( pi ) / 4 #. If one side of the triangle has a length of # 18 #, what is the longest possible perimeter of the triangle?

Question

1146 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-07-06T12:29:23

The perimeter is #=64.7u#

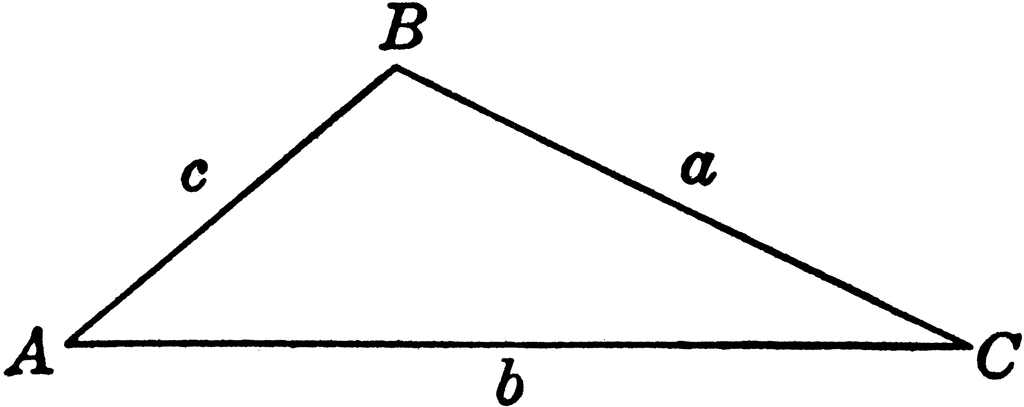
enter image source here

Let

#hatA=1/3pi#

#hatB=1/4pi#

So,

#hatC=pi-(1/3pi+1/4pi)=5/12pi#

The smallest angle of the triangle is #=1/4pi#

In order to get the longest perimeter, the side of length #18#

is #b=18#

We apply the sine rule to the triangle #DeltaABC#

#a/sin hatA=c/sin hatC=b/sin hatB#

#a/sin (1/3pi) = c/ sin(5/12pi)=18/sin(1/4pi)=25.5#

#a=25.5*sin (1/3pi)=22.1#

#c=25.5*sin(5/12pi)=24.6#

The perimeter of triangle #DeltaABC# is

#P=a+b+c=22.1+18+24.6=64.7#