Solve # sin x = 2cos^2x - 1 # where #x in [0,2pi]#?
2 Answers
# x= pi/6, (5pi)/6, (3pi)/2 #
Explanation:
We want to solve:
# sin x = 2cos^2x - 1 # where#x in [0,2pi]#
Using the identity
# sin x = 2(1-sin^2x) - 1 #
# " " = 2-2sin^2x- 1 #
# " " = 1-2sin^2x #
# :. 2sin^2x + sinx -1 = 0 #
Which is a quadratic in
# (2sinx -1)(sinx +1) = 0 #
Leading to two possible solution:
A)
# 2sinx -1 => sinx=1/2 #
B)# sinx+1 = 0 => sinx=-1 #
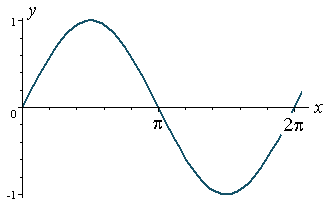
If we consider the graph of
Case (A):
# => x=pi/6, pi-pi/6#
# " " = pi/6, (5pi)/6#
Case (B):
# => x=(3pi)/2#
Hence, There are three solutions in the specified interval:
# x= pi/6, (5pi)/6, (3pi)/2 #
Explanation:
Bring the equation to standard form:
Since a - b + c = 0, use shortcut. The 2 real roots are:
Use trig table and unit circle -->
a. sin x = - 1 -->
b.